题目内容
【题目】(定义)数学课上,陈老师对我们说,如果1条线段将一个三角形分成2个等腰三角形,那么这1条线段就称为这个三角形的“好线”,如果2条线段将一个三角形分成3个等腰三角形,那么这2条线段就称为这个三角形的“好好线”.
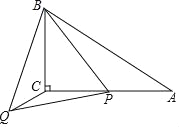
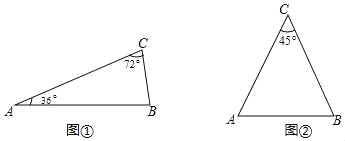
(理解)如图①,在△ABC中,∠A=36°,∠C=72°,请你在这个三角形中画出它的“好线”,并标出等腰三角形顶角的度数.
如图②,已知△ABC是一个顶角为45°的等腰三角形,请你在这个三角形中画出它的“好好线”,并标出所分得的等腰三角形底角的度数.
(应用)
(1)在△ABC中,已知一个内角为42°,若它只有“好线”,请你写出这个三角形最大内角的所有可能值______;
(2)在△ABC中,∠C=27°,AD和DE分别是△ABC的“好好线”,点D在BC边上,点E在AB边上,且AD=DC,BE=DE,请你根据题意画出示意图,并求∠B的度数.
【答案】【定义】见解析;【应用】(1)84°或103.5°或124°或117°或126°;(2)画图见解析;∠B=42°或18°.
【解析】
【定义】
如图①,如图②所示,根据题意画出图形即可;
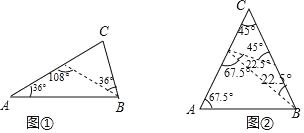
【应用】(1)①如图③当∠B=42°,AD为“好线”,②如图④当∠B=42°,AD为“好线”,③如图⑤当∠ABC=42°时,BD为“好线”,④如图⑥,当∠B=42°时,CD为“好线”,⑤如图⑦,当∠B=42°时,CD为“好线”,根据等腰三角形的性质即可得到结论;
(2)设∠B=x°,①当AD=DE时,如图1(a),②当AD=AE时,如图1(b),③当EA=DE时,根据等腰三角形的性质列方程即可得到结论.
解:(定义)如图①,如图②所示,
(应用)
(1)①如图③当∠B=42°,AD为“好线”,
则AD=AD=BD,故这个三角形最大内角是∠C=84°;
②如图④当∠B=42°,AD为“好线”,
则AB=AD,AD=CD,这个三角形最大内角是∠BAC=103.5°;
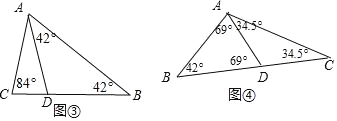
③如图⑤当∠ABC=42°时,BD为“好线”,
则AD=BD,CD=BC,故这个三角形最大内角是∠C=124°,
④如图⑥,当∠B=42°时,CD为“好线”,
则AD=CD=BC,故这个三角形最大内角是∠ACB=117°,
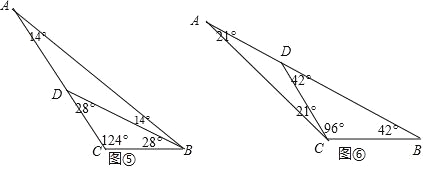
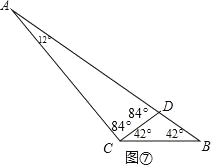
⑤如图⑦,当∠B=42°时,CD为“好线”,
则AD=AC,CD=BD,故这个三角形最大内角是∠ACB=126°,
综上所述,这个三角形最大内角的所有可能值是84°或103.5°或124°或117°或126°,
故答案为:84°或103.5°或124°或117°或126°;
(2)设∠B=x°,
①当AD=DE时,如图1(a),
∵AD=CD,
∴∠C=∠CAD=27°,
∵DE=EB,
∴∠B=∠EDB=x°
∴∠AED=∠DAE=2x°,
∴27×2+2x+x=180,
∴x=42,
∴∠B=42°;
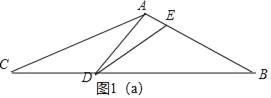
②当AD=AE时,如图1(b),
∵AD=CD,
∴∠C=∠CAD=27°,
∵DE=EB,
∴∠B=∠EDB=x°
∴∠AED=∠ADE=2x°,
∴2x+x=27+27,
∴x=18,
∴∠B=18°.
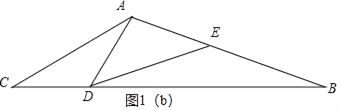
③当EA=DE时,
∵90﹣x+27+27+x=180,
∴x不存在,应舍去.
综合上述:满足条件的x=42°或18°.

 阅读快车系列答案
阅读快车系列答案【题目】为了鼓励市民节约用水,某市水费实行阶梯式计量水价.每户每月用水量不超过25吨,收
费标准为每吨a元;若每户每月用水量超过25吨时,其中前25吨还是每吨a元,超出的部
分收费标准为每吨b元.下表是小明家一至四月份用水量和缴纳水费情况.根据表格提供的数
据,回答:
月份 | 一 | 二 | 三 | 四 |
用水量(吨) | 16 | 18 | 30 | 35 |
水费(元) | 32 | 36 | 65 | 80 |
(1)a=________;b=________;
(2)若小明家五月份用水32吨,则应缴水费 元;
(3)若小明家六月份应缴水费102.5元,则六月份他们家的用水量是多少吨?