Question

【题目】已知两个等腰直角△ABC和△CDE，它们的两个直角顶点B、D在直线MN上，过点A、E分别作AG⊥MN，EF⊥MN，垂足分别为G、F．

(1)如图1，当△ABC和△CDE在△BCD的外部时，请你探索线段EF、DB、AG之间的数量关系，其数量关系为______．

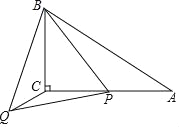
(2)如图2，将图1中的△ABC沿BC翻折，其他条件不变，那么(1)中的结论是否仍然成立？若成立，请你给出证明，若不成立，请探索它们的数量关系，并说明理由．

Answer 1

【答案】(1)BD＝EF+AG；(2)成立，证明见解析．

【解析】

（1）结论：BD=EF+AG．只要证明△FDE≌△HCD（AAS），可得EF=DH，同理可证：△BHC≌△AGB，可得AG=BH，即可解决问题；
（2）结论不变，证明方法类似；

解：(1)结论：BD＝EF+AG．

理由：如图1中，作CH⊥MN于H．

∵EF⊥MN，AG⊥MN，

∴∠EFD＝∠EDC＝∠CHD＝90°，

∴∠EDF+∠CDH＝90°，∠CDH+∠DCH＝90°，

∴∠EDF＝∠DCH，

∵DE＝DC，

∴△FDE≌△HCD(AAS)，

∴EF＝DH，

同理可证：△BHC≌△AGB，

∴AG＝BH，

∴BD＝EF+AG．

故答案为BD＝EF+AG．

(2)结论成立．

理由：如图2中，作CH⊥MN于H．

∵EF⊥MN，AG⊥MN，

∴∠EFD＝∠EDC＝∠CHD＝90°，

∴∠EDF+∠CDH＝90°，∠CDH+∠DCH＝90°，

∴∠EDF＝∠DCH，

∵DE＝DC，

∴△FDE≌△HCD(AAS)，

∴EF＝DH，

同理可证：△BHC≌△AGB，

∴AG＝BH，

∴BD＝EF+AG．

故答案为BD＝EF+AG．