题目内容
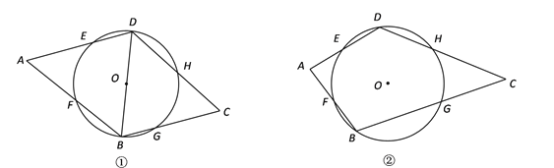
【题目】已知:如图,在同心圆中,大圆的弦AB交小圆于C、D两点.
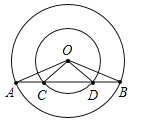
(1)求证:∠AOC=∠BOD;
(2)试确定AC与BD两线段之间的大小关系,并证明你的结论.
【答案】(1)证明见试题解析;(2)AC=BD,证明见试题解析.
【解析】
(1)由于OA=OB,OC=OD,利用等边对等角易得∠A=∠B,∠OCD=∠ODC,而利用三角形外角性质可得∠OCD=∠A+∠AOC,∠ODC=∠BOD+∠B,从而可得∠A+∠AOC=∠BOD+∠B,再利用等量相减,差相等可得∠AOC=∠DOB;
(2)过O作OE⊥AB于E,利用垂径定理有AE=EB,CE=ED,于是AE-CE=BE-DE,即AC=BD.
试题解析:
(1)∵AO=OB,OC=OD
∴∠A=∠B,∠OCD=∠ODC
∴∠OCA=∠ODC
∴△ACO≌△ODB
∴∠AOC=∠DOB
(2)过O作OE⊥AB于E
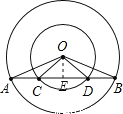
∴AE=EB,CE=ED
∴AC=BD

练习册系列答案
相关题目