��Ŀ����
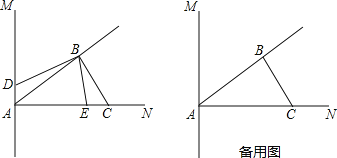
����Ŀ��ij������һ�鳤����ˮ�������������ij���������ͼ��ʾ�����ȵ�λ���ף���������������֣�һ����Ϊˮ������һ����Ϊ����ˮ����ֲ���Ӱ���֣���
��1���ú�a��b��ʽ�ӱ�ʾ����ˮ����ֲ�������Ƕ���ƽ���ף�������������ʽ����
��2����a��30��b��40������ũ����ս�������֮ʱˮ�����죬�ƻ����ɼ����ո���ո�һ���֣����������ո���ո�ʣ�ಿ�֣������ո���ո�ˮ��ÿƽ���ķ���Ϊ0.3Ԫ�������ո���ո�ˮ��ÿƽ���ķ���Ϊ0.5Ԫ����Ҫ�ո�ȫ��ˮ���ķ��ò�����5000Ԫ���ʼ����ո�������ո����ƽ����ˮ����

���𰸡���1��11b2��5ab����2�������ո�������ո�4000ƽ����ˮ����
��������
��1���ô���ε������ȥС���ε�����г���ʽ���ٻ��ɵã�
��2���Ƚ�a��b��ֵ���루1���л���Ĵ���ʽ���ˮ�����������������ո���ո�ˮ��aƽ���ף��������ո���ո�ˮ�����Ϊ��11600-a��ƽ���ף������ո�ȫ��ˮ���ķ��ò�����5000Ԫ�г�����ʽ����֮�ɵã�
��1������ˮ����ֲ������Ϊ��3b+b��a����2b+b��a������b��a��2
����4b��a����3b��a������b��a��2
��12b2��4ab��3ab+a2��b2+2ab��a2
��11b2��5ab��
��2����a��30��b��40ʱ������ˮ����ֲ������11b2��5ab��11600��ƽ���ף���
������ո���ո�ˮ��aƽ���ף��������ո���ո�ˮ�����Ϊ��11600��a��ƽ���ף�
�������⣬�ã�0.3a+0.5��11600��a����5000��
��ã�a��4000��
�𣺼����ո�������ո�4000ƽ����ˮ����

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ����ͨ����ѧ���۰��ڵ����·����ʻ����������������Һ�壬�����������ٶȡ��ܶ������������������Ļ�����������������q����/Сʱ��ָ��λʱ����ͨ����·ָ������ij��������ٶ�v��ǧ��/Сʱ��ָͨ����·ָ������ij����ٶȣ��ܶȣ���/ǧ�ף�ָͨ����·ָ�����浥λ�����ڵij�������Ϊ��ϴ������ζ��ж������ij·������q���ٶ�v֮��IJ����������±���
�ٶ�v��ǧ��/Сʱ�� | �� | 5 | 10 | 20 | 32 | 40 | 48 | �� |
����q����/Сʱ�� | �� | 550 | 1000 | 1600 | 1792 | 1600 | 1152 | �� |
��1�������ϱ���Ϣ����������������ϵʽ�У��̻�q��v��ϵ��ȷ������ֻ��������ȷ�𰸵���ţ��� ![]() ��
�� ![]() ��
�� ![]()
��2�������ã�1����ѡȡ�ĺ�����ϵʽ����������·�εij�����Ϊ����ʱ�������ﵽ�����������Ƕ��٣�
��3����֪q��v��k���� ![]() �����ϣ�1����ѡȡ�ĺ�����ϵʽ��������������⣺
�����ϣ�1����ѡȡ�ĺ�����ϵʽ��������������⣺
���н�ͨ���м��ƽ̨��ʾ���� ![]() ʱ��·�������ӵ�£��Է����������ܶ�k��ʲô��Χʱ����·�γ������ӵ�£�
ʱ��·�������ӵ�£��Է����������ܶ�k��ʲô��Χʱ����·�γ������ӵ�£�
��������״̬�£�����ǰ��������ͷ֮��ľ���d���ף�����ȣ�������q���ʱd��ֵ