题目内容
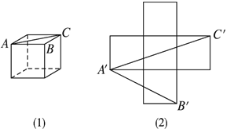
【题目】如图,在⊙O中,弦AD、BC相交于点E,连接OE,已知AD=BC,AD⊥CB.
(1)求证:AB=CD; (2)如果⊙O的半径为5,DE=1,求AE的长.

【答案】(1)详见解析;(2)7.
【解析】
(1)欲证明AB=CD,只需证得![]() =
=![]() ;
;
(2)如图,过O作OF⊥AD于点F,作OG⊥BC于点G,连接OA、OC.构建正方形EFOG,利用正方形的性质,垂径定理和勾股定理来求AF的长度,则易求AE的长度.
(1)证明:如图,∵AD=BC,
∴![]() =
=![]() ,
,
∴![]() ﹣
﹣![]() =
=![]() ﹣
﹣![]() ,即
,即![]() =
=![]() ,
,
∴AB=CD;
(2)如图,过O作OF⊥AD于点F,作OG⊥BC于点G,连接OA、OC.
则AF=FD,BG=CG.
∵AD=BC,
∴AF=CG.
在Rt△AOF与Rt△COG中,
![]() ,
,
∴Rt△AOF≌Rt△COG(HL),
∴OF=OG,
∴四边形OFEG是正方形,
∴OF=EF.
设OF=EF=x,则AF=FD=x+1,
在直角△OAF中.由勾股定理得到:x2+(x+1)2=52,
解得 x=3.
则AF=3+1=4,即AE=AF+3=7.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】宿州市高新区某电子电路板厂到安徽大学从2018年应届毕业生中招聘公司职员,对应聘者的专业知识、英语水平、参加社会实践与社团活动等三项进行测试或成果认定,三项的得分满分都为100分,三项的分数分别按5∶3∶2的比例记入每人的最后总分,有4位应聘者的得分如下表所示.
| 专业知识 | 英语水平 | 参加社会实践与 社团活动等 |
甲 | 85 | 85 | 90 |
乙 | 85 | 85 | 70 |
丙 | 80 | 90 | 70 |
丁 | 90 | 90 | 50 |
(1)分别算出4位应聘者的总分;
(2)表中四人“专业知识”的平均分为85分,方差为12.5,四人“英语水平”的平均分为87.5分,方差为6.25,请你求出四人“参加社会实践与社团活动等”的平均分及方差;
(3)分析(1)和(2)中的有关数据,你对大学生应聘者有何建议?