题目内容
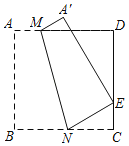
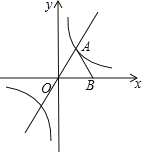
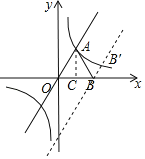
【题目】如图所示,在平面直角坐标系中,等边三角形OAB的一条边OB在x轴的正半轴上,点A在双曲线y=![]() (k≠0)上,其中点B为(2,0).
(k≠0)上,其中点B为(2,0).
(1)求k的值及点A的坐标
(2)△OAB沿直线OA平移,当点B恰好在双曲线上时,求平移后点A的对应点A’的坐标.
【答案】(1)A(1,![]() );k=
);k=![]() ;(2)点A′的坐标为(
;(2)点A′的坐标为(![]() ,
,![]() )或(﹣
)或(﹣![]() ,﹣
,﹣![]() ).
).
【解析】
(1)解直角三角形即可求得A点的坐标,根据反比例函数系数k的几何意义,即可求得k;
(2)求得直线OA的解析式,然后求得BB′解析式,联立方程解方程即可求得B′的坐标,进而求得A′的坐标.
(1)过A点作AC⊥OB于C,
∵△OAB是等边三角形,点B为(2,0),
∴OA=AB=OB=2,
∴OC=1,AC=![]() ,
,
∴A(1,![]() ),
),
∴k=1×![]() =
=![]() ,
,
(2)∵A(1,![]() ),
),
∴直线OA为y=![]() x
x
∵△OAB沿直线OA平移,
∴BB′∥OA,设直线BB′解析式为y=![]() x+b,
x+b,
把B(2,0)代入得,0=2![]() +b,
+b,
∴b=﹣2![]() ,
,
∴直线BB′解析式为y=![]() x﹣2
x﹣2![]() ,
,
解方程组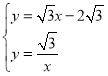 得
得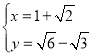 或
或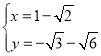 ,
,
∴平移后的点A′的坐标为(![]() ,
,![]() )或(﹣
)或(﹣![]() ,﹣
,﹣![]() ).
).

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目