题目内容
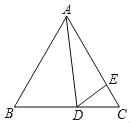
【题目】如图,以△ABC的一边AB为直径的半圆与其它两边AC,BC的交点分别为D,E,且弧DE=弧BE.
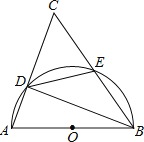
(1)试判断△ABC的形状,并说明理由;
(2)已知半圆的半径为5,BC=12,求BD的长.
【答案】(1)△ABC为等腰三角形,理由见解析;(2)![]()
【解析】
(1)连接AE,根据圆周角定理可得∠DAE=∠BAE,∠AEB=90°,再根据相等的角的余角也相等可得∠C=∠ABC,从而得到△ABC为等腰三角形;
(2)根据“三线合一”得到BE的长,利用勾股定理求得AE的长,再利用三角形的面积公式即可求得BD的长.
解:(1)△ABC为等腰三角形.
理由如下:连结AE,如图,
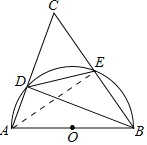
∵![]() ,
,
∴∠DAE=∠BAE,即AE平分∠BAC,
∵AB为直径,
∴∠AEB=90°,
∴AE⊥BC,
∵∠C+∠CAE=90°,∠ABC+∠BAE=90°,
∴∠C=∠ABC,
∴AC=AB,
∴△ABC为等腰三角形;
(2)∵△ABC为等腰三角形,AE⊥BC,
∴,![]() ,
,
在Rt△ABE中,
∵AB=10,BE=6,
∴![]() ,
,
∵AB为直径,
∴∠ADB=90°,
∴![]() ,
,
∴![]() .
.

练习册系列答案
相关题目