Question

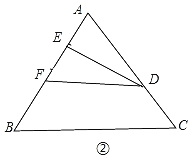
【题目】如图，在边长为3的等边△ABC中，点D在AC上，且CD＝1，点E在AB上（不与点A、B重合），连接DE，把△ADE沿DE折叠，当点A的对应点F落在等边△ABC的边上时，AE的长为_____．

Answer 1

【答案】1或5﹣．

【解析】

根据题意分类讨论，当F点落在边BC上时，证明△DFC∽△FEB，F点落在边AB上时，根据直角三角形的性质求解；

①当F点落在边BC上时，

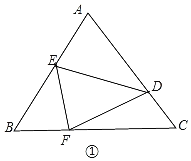
∵把△ADE沿DE折叠，

∴∠A＝∠EFD＝60°，

∵∠EFC＝∠B+∠BEF，

∴∠EFD+∠DFC＝∠B+∠BEF

∵∠EFD＝∠A＝∠B＝60°，

∴∠DFC＝∠BEF，

∴△DFC∽△FEB，

∴，

而EF+BE＝EA+BE＝AB＝3，DF＝DA＝AC﹣CD＝2，

∴，

解得AE＝5﹣，或AE＝5+（舍去）；

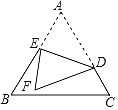
②F点落在边AB上时，

∵把△ADE沿DE折叠，

∴∠A＝∠DFE＝60°，∠DEA＝90°，∠ADE＝∠FDE，

∴∠ADE＝30°，

∴AE＝AD＝（AC﹣CD）＝×2＝1．

故A答案为1或5﹣．