题目内容
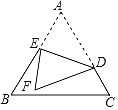
【题目】如图,在平面直角坐标系中,直线y=﹣![]() x+3与y轴交于点A,与x轴交于点B,抛物线y=﹣
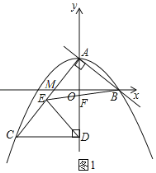
x+3与y轴交于点A,与x轴交于点B,抛物线y=﹣![]() x2+bx+c经过点A和点B,过点A作AC⊥AB交抛物线于点C,过点C作CD⊥y轴于点D,点E在线段AC上,连接ED,且ED=EC,连接EB交y轴于点F.
x2+bx+c经过点A和点B,过点A作AC⊥AB交抛物线于点C,过点C作CD⊥y轴于点D,点E在线段AC上,连接ED,且ED=EC,连接EB交y轴于点F.
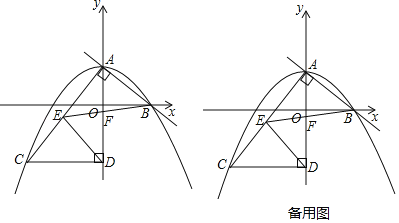
(1)求抛物线的表达式;
(2)求点C的坐标;
(3)若点G在直线AB上,连接FG,当∠AGF=∠AFB时,直接写出线段AG的长;
(4)在(3)的条件下,点H在线段ED上,点P在平面内,当△PAG≌△PDH时,直接写出点P的坐标.
【答案】(1)y=﹣![]() x2+
x2+![]() x+3;(2)C(﹣6,﹣5);(3)
x+3;(2)C(﹣6,﹣5);(3)![]() ;(4)P(
;(4)P(![]() ,﹣1)
,﹣1)
【解析】
(1)先求出点A,B坐标,再代入抛物线解析式中,即可得出结论;
(2)先判断出△AOB∽△MOA,得出![]() ,求出
,求出![]() ,进而得出直线AM的解析式为
,进而得出直线AM的解析式为![]() ,直线AM和抛物线解析式联立求解即可得出结论;
,直线AM和抛物线解析式联立求解即可得出结论;
(3)先判断出∠EAF=∠BFG,进而判断出△AFE∽△FGB,得出![]() ,再求出EF=
,再求出EF=![]() ,BF=
,BF=![]() ,即可得出结论;
,即可得出结论;
(4)先判断出∠PAG=∠PDH,PA=PD,进而判断出点P在AD的垂直平分线上,设P(m,﹣1),再判断出△APB≌△DPE(SAS),得出PE=BP,利用PE=PB建立方程求解即可得出结论.
解:针对于直线y=﹣![]() x+3,
x+3,
令x=0,则y=3,
∴A(0,3),
令y=0,
则0=﹣![]() x+3,
x+3,
∴x=4,
∴B(4,0),
将点A(0,3),B(4,0)代入抛物线y=﹣![]() x2+bx+c中,得
x2+bx+c中,得 ,
,
∴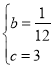 ,
,
∴抛物线的解析式为y=﹣![]() x2+
x2+![]() x+3;
x+3;
(2)如图1,设AC与x轴的交点为M,
∵AC⊥AB,
∴∠OAM+∠OAB=90°,
∵∠OBA+∠OAB=90°,
∴∠OAM=∠OBA,
∵∠AOB=∠MOA=90°,
∴△AOB∽△MOA,
∴![]() ,
,
∴MO=![]() =
=![]() ,
,
∴M(﹣![]() ,0),
,0),
∵A(0,3),
∴直线AM的解析式为y=![]() x+3①,
x+3①,
由(1)知,抛物线的解析式为y=﹣![]() x2+
x2+![]() x+3②,
x+3②,
联立①②解得,![]() 或
或![]() ,
,
∴C(﹣6,﹣5);
(3)如图2,
∵CD⊥y轴,EC=ED,
∴点E是CD的垂直平分线上,
∴点E在AC上,
∴E(﹣3,﹣1),
由(1)知,A(0,3),B(4,0),
∴AB=5,AE=5,
∴AB=AE,
∴∠AEO=∠ABO=45°,
∴∠AFB=∠AEO+∠OAE=45°+∠OAE,∠AGF=∠ABO+∠BFG=45°+∠BFG,
∵∠AGF=∠AFB,
∴∠EAF=∠BFG,
∵∠AEF=∠FBG=45°,
∴△AFE∽△FGB,
∴![]() ,
,
∴BG=![]() ,
,
∵B(4,0),E(﹣3,﹣1),
∴直线BE的解析式为y=![]() x﹣
x﹣![]() ,
,
∴F(0,﹣![]() ),
),
∴EF=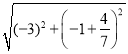 =
=![]() ,BF=
,BF=![]() ,
,
∴BG=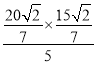 =
=![]() ,
,
∴AG=AB﹣BG=![]() ;
;
(4)如图3,
∵△PAG≌△PDH,
∴∠PAG=∠PDH,PA=PD,
∵PA=PD,
∴点P在AD的垂直平分线上,
∵A(0,3),
∴设P(m,﹣1),
连接BP,PE,
∴PE=m+3,BP=![]() ,
,
∵D(0,﹣5),E(﹣3,﹣1),
∴DE=5=AB,
在△APB和△DPE中,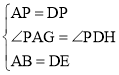 ,
,
∴△APB≌△DPE(SAS),
∴PE=BP,
∴m+3=![]() ,
,
∴m=![]() ,
,
∴P(![]() ,﹣1).
,﹣1).