题目内容
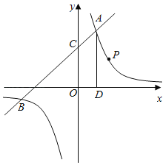
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于点
的图象交于点![]() 和
和![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)![]() ,
,![]() ;
;
(2)根据函数图象知,
①当![]() 时,
时,![]() 的取值范围是 ;
的取值范围是 ;
②当![]() 为 时,
为 时,![]() .
.
(3)过点![]() 作
作![]() 轴于点
轴于点![]() ,点
,点![]() 是反比例函数在第一象限的图象上一点,设直线
是反比例函数在第一象限的图象上一点,设直线![]() 与线段
与线段![]() 交于点
交于点![]() ,当
,当![]() 时,求点
时,求点![]() 的坐标.
的坐标.
(4)点![]() 是
是![]() 轴上的一个动点,当△MBC为直角三角形时,直接写出点
轴上的一个动点,当△MBC为直角三角形时,直接写出点![]() 的坐标.
的坐标.
【答案】(1)1,12;(2)①![]() 或
或![]() ;②
;②![]() ;(3)
;(3)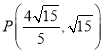 ;(4)点M的坐标为
;(4)点M的坐标为![]() 或
或![]() .
.
【解析】
(1)根据点![]() 的坐标,利用待定系数法即可求出
的坐标,利用待定系数法即可求出![]() 、
、![]() 的值;
的值;
(2)观察两函数图象的上下位置关系,由此即可得出不等式的解集;
(3)根据一次函数图象上点的坐标特征求出点![]() 、
、![]() 的坐标,根据梯形的面积公式求出
的坐标,根据梯形的面积公式求出![]() 的值,进而即可得出
的值,进而即可得出![]() 的值,结合三角形的面积公式即可得出点
的值,结合三角形的面积公式即可得出点![]() 的坐标,利用待定系数法即可求出直线
的坐标,利用待定系数法即可求出直线![]() 的解析式,再联立直线
的解析式,再联立直线![]() 与反比例函数的解析式成方程组,通过解方程组求出点
与反比例函数的解析式成方程组,通过解方程组求出点![]() 的坐标;
的坐标;
(4)分![]() 或
或![]() 两种情况考虑,当
两种情况考虑,当![]() 时,根据点
时,根据点![]() 的坐标即可找出点
的坐标即可找出点![]() 的坐标;当
的坐标;当![]() 时,由直线
时,由直线![]() 的解析式可得出
的解析式可得出![]() 为等腰直角三角形,根据等腰直角三角形的性质结合点
为等腰直角三角形,根据等腰直角三角形的性质结合点![]() 、
、![]() 的坐标即可得出点
的坐标即可得出点![]() 的坐标.综上即可得出结论.
的坐标.综上即可得出结论.
解:(1)将点![]() 代入
代入![]() ,
,
![]() ,解得:
,解得:![]() ;
;
将点![]() 代入
代入![]() ①,
①,
![]() ,解得:
,解得:![]() .
.
故答案为:1;12.
(2)①观察函数图象可知:当![]() 或
或![]() 时,一次函数图象在反比例函数图象上方,
时,一次函数图象在反比例函数图象上方,
![]() 当
当![]() 时,
时,![]() 的取值范围是
的取值范围是![]() 或
或![]() .
.
故答案为:![]() 或
或![]() .
.
②过点![]() 作直线
作直线![]() ,如图1所示.
,如图1所示.
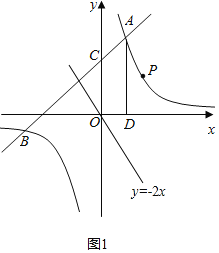
观察图形可知:![]() 时,反比例函数图象在直线
时,反比例函数图象在直线![]() 上方,
上方,
故答案为:![]() .
.
(3)依照题意,画出图形,如图2所示.
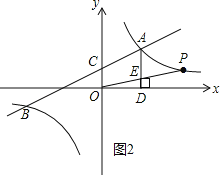
当![]() 时,
时,![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() ;
;
当![]() 时,
时,![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() .
.
![]() ,
,![]() ,
,
![]() ,
,
![]() ,即点
,即点![]() 的坐标为
的坐标为![]() .
.
设直线![]() 的解析式为
的解析式为![]() ,
,
将点![]() 代入
代入![]() ,得
,得
![]() ,解得:
,解得:![]() ,
,
![]() 直线
直线![]() 的解析式为
的解析式为![]() ②.
②.
联立①②并解得: ,
,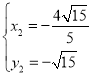 ,
,
![]() 点
点![]() 在第一象限,
在第一象限,
![]() 点
点![]() 的坐标为
的坐标为![]() .
.
(4)依照题意画出图形,如图3所示.
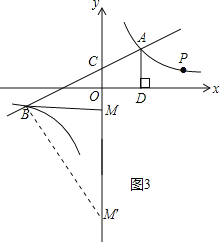
当![]() 时,
时,![]() 轴,
轴,
![]() 点
点![]() 的坐标为
的坐标为![]() ;
;
当![]() 时,
时,
![]() 直线
直线![]() 的解析式为
的解析式为![]() ,
,
![]() ,
,
![]() 为等腰直角三角形,
为等腰直角三角形,
![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() .
.
综上所述:当![]() 为直角三角形时,点
为直角三角形时,点![]() 的坐标为
的坐标为![]() 或
或![]() .
.