Question

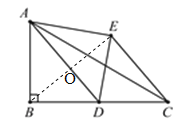
【题目】如图，在Rt△ABC中，AB=3，BC=8，点D为BC的中点，将△ABD沿AD折叠，使点B落在点E处，连接CE，则CE的长为_________.

Answer 1

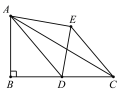
【答案】6.4（或）

【解析】

连接BE交AD于O．在Rt△ABD中，由勾股定理求出AD的长．由折叠的性质得到AB=AE，BD=DE，从而得到AD是线段BE的垂直平分线，即有BO=OE，AD⊥BE．

由△ABD的面积，求出BO的长，得到BE的长．再由BD=DE=DC证明△BEC是直角三角形，利用勾股定理即可得出结论．

连接BE交AD于O．

∵BC=8，点D为BC的中点，∴BD=DC=4．

∵∠ABD=90°，AB=3，BD=4，∴AD=5．

∵△ABD≌△AED（折叠的性质），∴AB=AE，BD=DE，∴AD是线段BE的垂直平分线，∴BO=OE，AD⊥BE．

∵△ABD的面积=ABBD=ADBO，∴BO===2.4，∴BE=2BO=4.8．

∵BD=DE，∴∠DBE=∠DEB．

∵ED=DC=4，∴∠DEC=∠DCE．

∵∠DBE+∠BED+∠DEC+∠DCE=180°，∴2∠BED+2∠DEC=180°，∴∠BEC=∠BED+∠DEC=90°，∴EC===6.4．

故答案为：6.4．