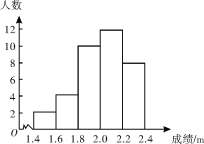
题目内容
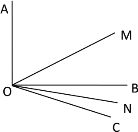
【题目】如图1,O为直线AB上一点,过点O作射线OC,∠AOC=30°,将一直角三角尺(∠M=30°)的直角顶点放在点O处,一边ON在射线OA上,另一边OM与OC都在直线AB的上方.
(1)若将图1中的三角尺绕点O以每秒5°的速度,沿顺时针方向旋转t秒,当OM恰好平分∠BOC时,如图2.
①求t值;
②试说明此时ON平分∠AOC;
(2)将图1中的三角尺绕点O顺时针旋转,设∠AON=α,∠COM=β,当ON在∠AOC内部时,试求α与β的数量关系;
(3)若将图1中的三角尺绕点O以每秒5°的速度沿顺时针方向旋转的同时,射线OC也绕点O以每秒8°的速度沿顺时针方向旋转,如图3,那么经过多长时间,射线OC第一次平分∠MON?请说明理由.

【答案】(1)①t=3;②见解析;(2)β=α+60°;(3)t=5时,射线OC第一次平分∠MON.
【解析】
(1)根据角平分线的性质以及余角补角的性质即可得出结论;
(2)根据∠NOC=∠AOC-∠AON=90°-∠MOC即可得到结论;
(3)分别根据转动速度关系和OC平分∠MON列方程求解即可.
(1)①∵∠AOC=30°,OM平分∠BOC,∴∠BOC=2∠COM=2∠BOM=150°,∴∠COM=∠BOM=75°.
∵∠MON=90°,∴∠CON=15°,∠AON+∠BOM=90°,∴∠AON=∠AOC﹣∠CON=30°﹣15°=15°,∴∠AON=∠CON,∴t=15°÷3°=5秒;
②∵∠CON=15°,∠AON=15°,∴ON平分∠AOC.
(2)∵∠AOC=30°,∴∠NOC=∠AOC-∠AON=90°-∠MOC,∴30°-α=90°-β,∴β=α+60°;
(3)设旋转时间为t秒,∠AON=5t,∠AOC=30°+8t,∠CON=45°,∴30°+8t=5t+45°,∴t=5.
即t=5时,射线OC第一次平分∠MON.

 每课必练系列答案
每课必练系列答案