题目内容
【题目】如图,点A,B,C在⊙O上,∠ABC=29°,过点C作⊙O的切线交OA的延长线于点D,则∠D的大小为( )
A.29°
B.32°
C.42°
D.58°
【答案】B
【解析】解:作直径B′C,交⊙O于B′,连接AB′,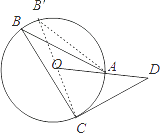
则∠AB′C=∠ABC=29°,
∵OA=OB′,
∴∠AB′C=∠OAB′=29°.
∴∠DOC=∠AB′C+∠OAB′=58°.
∵CD是⊙的切线,
∴∠OCD=90°.
∴∠D=90°﹣58°=32°.
故答案为:B.
根据切线的性质圆的切线垂直于经过切点的半径可作辅助线,作直径B′C,交⊙O于B′,连接AB′,则∠OCD=90°.由同弧所对的圆周角相等可得∠AB′C=∠ABC,∠DOC的度数可求,由直角三角形两锐角互余可求∠D的度数。

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目





