题目内容
【题目】如图,一次函数![]() 的图象分别与
的图象分别与![]() 轴,
轴,![]() 轴交于
轴交于![]() ,以线段
,以线段![]() 为边在第一象限内作等腰直角三角形
为边在第一象限内作等腰直角三角形![]() ,使
,使![]() .
.
(1)分别求点![]() 的坐标;
的坐标;
(2)在![]() 轴上求一点
轴上求一点![]() ,使它到
,使它到![]() 两点的距离之和最小.
两点的距离之和最小.

【答案】(1) B的坐标是(0,2),C的坐标是(5,3);(2) P(2,0).
【解析】
(1)先根据一次函数的解析式求出A、B两点的坐标,再作CD⊥x轴于点D,由全等三角形的判定定理可得出△ABO≌△CAD,由全等三角形的性质可知OA=CD,故可得出C点坐标;
(2)求得B点关于x轴的对称点B'的坐标,连接B'C与x轴的交点即为所求的P点,由B'、C坐标可求得直线B'C的解析式,则可求得P点坐标.
解:∵一次函数![]() 中,令x=0得:y=2;
中,令x=0得:y=2;
令y=0,解得x=3.
∴B的坐标是(0,2),A的坐标是(3,0).
作CD⊥x轴于点D.
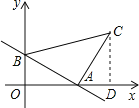
∵∠BAC=90°,
∴∠OAB+∠CAD=90°,
又∵∠CAD+∠ACD=90°,
∴∠ACD=∠BAO,
又∵AB=AC,∠BOA=∠CDA=90°,
∴△ABO≌△CAD(AAS),
∴AD=OB=2,CD=OA=3,OD=OA+AD=5.
则C的坐标是(5,3).
(2)如图,作点B关于x轴的对称点B',连接CB'交x轴于P,此时PB+PC的值最小.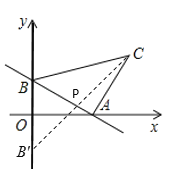
∵B(0,2),C(5,3)
∴B'(0,-2),
设直线C B'的解析式为y=kx+b,
把(0,-2) (5,3)代入y=kx+b中,
可得:![]() ,
,
解得:![]() ,
,
∴直线CB'的解析式为y=x-2,
令y=0,得到x=2,
∴P(2,0).

练习册系列答案
相关题目