题目内容
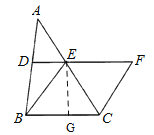
【题目】如图,在![]() 中,
中,![]() 分别是
分别是![]() ,
,![]() 的中点,
的中点,![]() ,延长
,延长![]() 到点F,使得
到点F,使得![]() ,连结
,连结![]() .
.

(1)求证:四边形![]() 是菱形;
是菱形;
(2)若![]() ,
,![]() ,求菱形
,求菱形![]() 的面积.
的面积.
【答案】(1)见解析;(2)![]()
【解析】
(1)从所给的条件可知,DE是△ABC的中位线,所以DE∥BC且2DE=BC,所以BC和EF平行且相等,所以四边形BCFE是平行四边形,又因为BE=EF,所以是菱形;
(2)由∠BEF是120°,可得∠EBC为60°,即可得△BEC是等边三角形,求得BE=BC=CE=5,再过点E作EG⊥BC于点G,求出高EG的长,即可求得答案.
解:(1)∵D、E分别是AB、AC的中点,
∴DE∥BC且2DE=BC,
又∵BE=2DE,EF=BE,
∴EF=BC,EF∥BC,
∴四边形BCFE是平行四边形,
又∵BE=EF,
∴四边形BCFE是菱形;
(2)∵∠BEF=120°,
∴∠EBC=60°,
∴△EBC是等边三角形,
∴BE=BC=CE=5,
过点E作EG⊥BC于点G,
∴EG=BEsin60°=5×![]() ,
,
∴S菱形BCFE=BCEG=5×![]() .
.

练习册系列答案
相关题目