��Ŀ����
����Ŀ����ͼ�٣���Rt��ABC�У���C=90�㣬AB=10��BC=6����P�ӵ�A������������AB��BC���յ�C�˶�����AB����ÿ��5����λ���ȵ��ٶ��˶�����BC����ÿ��3����λ���ȵ��ٶ��˶�����Q�ӵ�C��������CA������ÿ��![]() ����λ���ȵ��ٶ��˶���P��Q����ͬʱ����������Pֹͣʱ����QҲ��ֹ֮ͣ�����P�˶���ʱ��Ϊt�룮
����λ���ȵ��ٶ��˶���P��Q����ͬʱ����������Pֹͣʱ����QҲ��ֹ֮ͣ�����P�˶���ʱ��Ϊt�룮
��1�����߶�AQ�ij������ú�t�Ĵ���ʽ��ʾ��
��2������PQ����PQ���ABC��һ��ƽ��ʱ����t��ֵ��
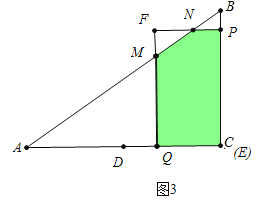
��3����ͼ�ڣ�����P��PE��AC�ڵ�E����PE��EQΪ�ڱ�������PEQF����DΪAC���е㣬����DF�������PEQF���ABC�ص�����ͼ�ε����ΪS��
�ٵ���Q���߶�CD���˶�ʱ����S��t֮��ĺ�����ϵʽ��
��ֱ��д��DF������PEQF�ֳ������ֵ������Ϊ1��2ʱt��ֵ��

���𰸡���1��AQ=8��![]() t��0��t��4������2��t=
t��0��t��4������2��t=![]() s��3s����3����
s��3s����3����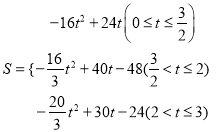 ����t=
����t=![]() s��
s��![]() s��
s��
�������������������1�����ù��ɶ��������AC������AQ=AC��CQ���ɽ�����⣻
��2�������������г�������⼴�ɣ�
��3��������������a����ͼ1�У���0��t��![]() ʱ���ص��������ı���PEQF��b����ͼ2�У���
ʱ���ص��������ı���PEQF��b����ͼ2�У���![]() ��t��2ʱ���ص��������ı���PNQE��C����ͼ3�У���2��t��3ʱ���ص������������MNPBQ���ֱ���⼴�ɣ�
��t��2ʱ���ص��������ı���PNQE��C����ͼ3�У���2��t��3ʱ���ص������������MNPBQ���ֱ���⼴�ɣ�
������������a����ͼ4�У���DE��DQ=1��2ʱ��DF������PEQF�ֳ������ֵ������Ϊ1��2��b����ͼ5�У���NE��PN=1��2ʱ��DF������PEQF�ֳ������ֵ������Ϊ1��2���ֱ��г����̼��ɽ�����⣻
����������⣺��1����Rt��ABC�У��ߡ�C=90����AB=10��BC=6����AC=![]() =
=![]() =8����CQ=
=8����CQ=![]() t����AQ=8��
t����AQ=8��![]() t��0��t��4����
t��0��t��4����
��2������PQ��BCʱ�� ![]() ����
���� ����t=
����t=![]() s��
s��
����PQ��ABʱ�� ![]() ����
���� ����t=3��
����t=3��
����������t=![]() s��3sʱ����PQ����ABC��һ��ƽ�У�
s��3sʱ����PQ����ABC��һ��ƽ�У�
��3������ͼ1�У�a����0��t��![]() ʱ���ص��������ı���PEQF��
ʱ���ص��������ı���PEQF��
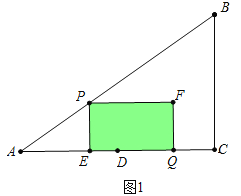
S=PEEQ=3t��8��4t��![]() t��=
t��=![]() ��
��
b����ͼ2�У���![]() ��t��2ʱ���ص��������ı���PNQE��
��t��2ʱ���ص��������ı���PNQE��
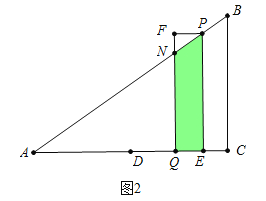
S=S�ı���PEQF��S��PFN=��16t2��24t����![]()
![]() [5t��
[5t��![]() ��8��
��8��![]() t��]
t��] ![]() [5t��
[5t��![]() ��8��
��8��![]() t0]=
t0]= ![]() ��
��
C����ͼ3�У���2��t��3ʱ���ص������������MNPBQ��
S =S�ı���PBQF -S��FNM=![]() t[6��3��t��2��]��
t[6��3��t��2��]��![]() [
[![]() t��4��t��2��]
t��4��t��2��] ![]() [
[![]() t��4��t��2��]=
t��4��t��2��]= ![]() ��
��
���������� 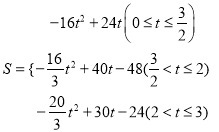 ��
��
��a����ͼ4�У���DE��DQ=1��2ʱ��DF������PEQF�ֳ������ֵ������Ϊ1��2��
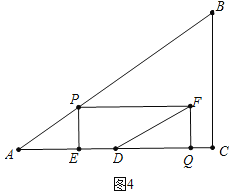
����4��4t������4��![]() t��=1��2�����t=
t��=1��2�����t=![]() s��
s��
b����ͼ5�У���NE��PN=1��2ʱ��DF������PEQF�ֳ������ֵ������Ϊ1��2��
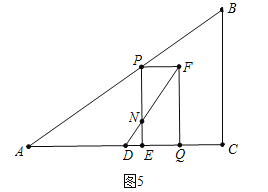
��DE��DQ=NE��FQ=1��3������4t��4������4��![]() t��=1��3�����t=
t��=1��3�����t=![]() s��
s��
������������t=![]() s��
s��![]() sʱ��DF������PEQF�ֳ������ֵ������Ϊ1��2��
sʱ��DF������PEQF�ֳ������ֵ������Ϊ1��2��

 ������ҵ����ν�����������ϵ�д�
������ҵ����ν�����������ϵ�д�






