��Ŀ����
����Ŀ�����壺���ڸ�����������������ȡ�Ա���x��һ��ֵ����x��0ʱ�����Ƕ�Ӧ�ĺ���ֵ��Ϊ�෴������x��0ʱ�����Ƕ�Ӧ�ĺ���ֵ��ȣ����dz�����������������Ϊ��غ��������磺һ�κ���y=x��1��������غ���Ϊ ��
��
��1����֪��A����5��8����һ�κ���y=ax��3����غ�����ͼ���ϣ���a��ֵ��
��2����֪���κ���![]() ��
��
�ٵ���B��m�� ![]() ���������������غ�����ͼ����ʱ����m��ֵ��
���������������غ�����ͼ����ʱ����m��ֵ��
�ڵ���3��x��3ʱ������![]() ����غ��������ֵ����Сֵ��
����غ��������ֵ����Сֵ��
��3����ƽ��ֱ������ϵ�У���M��N������ֱ�Ϊ����![]() ��1������
��1������![]() ��1}��������MN��ֱ��д���߶�MN����κ���
��1}��������MN��ֱ��д���߶�MN����κ���![]() ����غ�����ͼ��������������ʱn��ȡֵ��Χ��
����غ�����ͼ��������������ʱn��ȡֵ��Χ��
���𰸡���1��1����2����m=2��![]() ��m=2+
��m=2+![]() ��m=2��
��m=2��![]() �������ֵΪ
�������ֵΪ![]() ����СֵΪ��
����СֵΪ��![]() ����3����3��n�ܩ�1��1��n��
����3����3��n�ܩ�1��1��n��![]() ��
��
�������������������1������y=ax��3����غ���Ϊ![]() ����Ȼ��A����5��8������y=��ax+3��⼴�ɣ�
����Ȼ��A����5��8������y=��ax+3��⼴�ɣ�
��2�����κ���![]() ����غ���Ϊ
����غ���Ϊ ������Ϊm��0��m��0�����������B����������Ӧ�Ĺ�ϵʽ��⼴�ɣ�������3��x��0ʱ��
������Ϊm��0��m��0�����������B����������Ӧ�Ĺ�ϵʽ��⼴�ɣ�������3��x��0ʱ�� ![]() ��Ȼ��� ��ʱ�����ֵ����Сֵ����0��x��3ʱ������
��Ȼ��� ��ʱ�����ֵ����Сֵ����0��x��3ʱ������![]() ����ô�ʱ�����ֵ����Сֵ���Ӷ��ɵõ�����3��x��3ʱ�����ֵ����Сֵ��
����ô�ʱ�����ֵ����Сֵ���Ӷ��ɵõ�����3��x��3ʱ�����ֵ����Сֵ��
��3������ȷ�������κ���![]() ����غ������߶�MNǡ����1�����㡢2�����㡢3������ʱn��ֵ��Ȼ���Ϻ���ͼ���ȷ����n��ȡֵ��Χ��
����غ������߶�MNǡ����1�����㡢2�����㡢3������ʱn��ֵ��Ȼ���Ϻ���ͼ���ȷ����n��ȡֵ��Χ��
����������⣺��1������y=ax��3����غ���Ϊ![]() ������A����5��8������y=��ax+3�ã�5a+3=8����ã�a=1��
������A����5��8������y=��ax+3�ã�5a+3=8����ã�a=1��
��2�����κ���![]() ����غ���Ϊ
����غ���Ϊ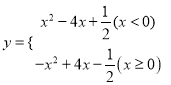 ��
��
����m��0ʱ����B��m�� ![]() ������
������![]() ��
��![]() ����ã�m=2+
����ã�m=2+![]() ����ȥ����m=2��
����ȥ����m=2��![]() ��
��
��m��0ʱ����B��m�� ![]() ������
������![]() �ã�
�ã� ![]() ����ã�m=2+
����ã�m=2+![]() ��m=2��
��m=2��![]() ��
��
����������m=2��![]() ��m=2+
��m=2+![]() ��m=2��
��m=2��![]() ��
��
������3��x��0ʱ�� ![]() �������ߵĶԳ���Ϊx=2����ʱy��x���������С������ʱy�����ֵΪ
�������ߵĶԳ���Ϊx=2����ʱy��x���������С������ʱy�����ֵΪ![]() ��
��
��0��x��3ʱ������![]() �������ߵĶԳ���Ϊx=2����x=0����Сֵ����СֵΪ��
�������ߵĶԳ���Ϊx=2����x=0����Сֵ����СֵΪ��![]() ����x=2ʱ�������ֵ�����ֵy=
����x=2ʱ�������ֵ�����ֵy=![]() ��
��
��������������3��x��3ʱ������![]() ����غ��������ֵΪ
����غ��������ֵΪ![]() ����СֵΪ��
����СֵΪ��![]() ��
��
��3����ͼ1��ʾ���߶�MN����κ���![]() ����غ�����ͼ��ǡ��1�������㣮
����غ�����ͼ��ǡ��1�������㣮
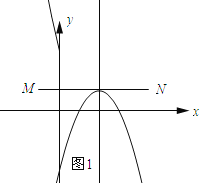
���Ե�x=2ʱ��y=1������4+8+n=1�����n=��3��
��ͼ2��ʾ���߶�MN����κ���![]() ����غ�����ͼ��ǡ��3��������
����غ�����ͼ��ǡ��3��������

��������![]() ��y�ύ��������Ϊ1������n=1����ã�n=��1��������3��n�ܩ�1ʱ���߶�MN����κ���
��y�ύ��������Ϊ1������n=1����ã�n=��1��������3��n�ܩ�1ʱ���߶�MN����κ���![]() ����غ�����ͼ��ǡ��2�������㣮
����غ�����ͼ��ǡ��2�������㣮
��ͼ3��ʾ���߶�MN����κ���![]() ����غ�����ͼ��ǡ��3�������㣮
����غ�����ͼ��ǡ��3�������㣮
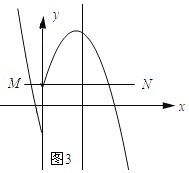
��������![]() �����㣨0��1������n=1��
�����㣨0��1������n=1��
��ͼ4��ʾ���߶�MN����κ���![]() ����غ�����ͼ��ǡ��2�������㣮
����غ�����ͼ��ǡ��2�������㣮

��������![]() ������M����
������M����![]() ��1������
��1������![]() +2��n=1����ã�n=
+2��n=1����ã�n=![]() ����1��n��
����1��n��![]() ʱ���߶�MN����κ���
ʱ���߶�MN����κ���![]() ����غ�����ͼ��ǡ��2�������㣮
����غ�����ͼ��ǡ��2�������㣮
����������n��ȡֵ��Χ�ǩ�3��n����1��1��n��![]() ��
��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�


