题目内容
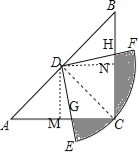
【题目】如图,在△ABC中,CA=CB,∠ACB=90°,以AB的中点D为圆心,作圆心角为90°的扇形DEF,点C恰在EF上,设∠BDF=α(0°<α<90°),当α由小到大变化时,图中阴影部分的面积( )

A. 由小到大 B. 由大到小 C. 不变 D. 先由小到大,后由大到小
【答案】C
【解析】试题分析:作DM⊥AC于M,DN⊥BC于N,构造正方形DMCN,利用正方形和等腰直角三角形的性质,通过证明△DMG≌△DNH,把△DHN补到△DNG的位置,得到四边形DGCH的面积=正方形DMCN的面积,于是得到阴影部分的面积=扇形的面积﹣正方形DMCN的面积,即为定值.
试题解析:解:作DM⊥AC于M,DN⊥BC于N,连接DC,
∵CA=CB,∠ACB=90°,
∴∠A=∠B=45°,
DM=![]() AD=
AD=![]() AB,DN=
AB,DN=![]() BD=
BD=![]() AB,
AB,
∴DM=DN,
∴四边形DNCN是正方形,
∴∠MDN=90°,
∴∠MDG=90°﹣∠GDN,
∵∠EDF=90°,
∴∠NDH=90°﹣∠GDN,
∴∠MDG=∠NDH,
在△DMG和△DNH中,
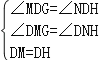 ,
,
∴△DMG≌△DNH,
∴四边形DGCH的面积=正方形DMCN的面积,
∵正方形DMCN的面积=DM2=![]() AB2,
AB2,
∴四边形DGCH的面积=![]() ,
,
∵扇形FDE的面积=![]() =
=![]() ,
,
∴阴影部分的面积=扇形面积﹣四边形DGCH的面积=![]() (定值),
(定值),
故选C.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目



