题目内容
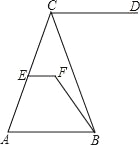
【题目】如图,已知点E、F在直线AB上,点G在线段CD上,ED与FG交于点H,∠C=∠EFG,∠CED=∠GHD.
(1)求证:CE∥GF;
(2)试判断∠AED与∠D之间的数量关系,并说明理由;
(3)若∠EHF=80°,∠D=30°,求∠AEM的度数.
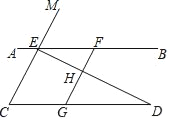
【答案】(1)证明见解析;(2)∠AED+∠D=180°,理由见解析;(3)110°
【解析】
(1)依据同位角相等,即可得到两直线平行;
(2)依据平行线的性质,可得出∠FGD=∠EFG,进而判定AB∥CD,即可得出∠AED+∠D=180°;
(3)依据已知条件求得∠CGF的度数,进而利用平行线的性质得出∠CEF的度数,依据对顶角相等即可得到∠AEM的度数.
(1)∵∠CED=∠GHD,
∴CB∥GF;
(2)∠AED+∠D=180°;
理由:∵CB∥GF,
∴∠C=∠FGD,
又∵∠C=∠EFG,
∴∠FGD=∠EFG,
∴AB∥CD,
∴∠AED+∠D=180°;
(3)∵∠GHD=∠EHF=80°,∠D=30°,
∴∠CGF=80°+30°=110°,
又∵CE∥GF,
∴∠C=180°﹣110°=70°,
又∵AB∥CD,
∴∠AEC=∠C=70°,
∴∠AEM=180°﹣70°=110°.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目