Question

【题目】如图，BD是△ABC的角平分线，过点D作DE∥BC交AB于点E，DF∥AB交BC于点F．

⑴求证:四边形BEDF为菱形;

⑵如果∠A＝100°,∠C＝30°,求∠BDE的度数.

Answer 1

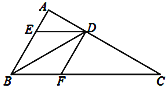
【答案】（1）证明见解析（2）25°

【解析】

(1)首先证明四边形DEBF是平行四边形，根据平行线的性质得到∠EDB＝∠DBF，根据角平分线的性质得到∠ABD＝∠DBF，等量代换得到∠ABD＝∠EDB，得到DE＝BE，即可证明四边形BEDF为菱形；

⑵根据三角形的内角和求出的度数，根据角平分线的性质得到的度数，根据平行线的性质即可求解.

（1）∵DE∥BC，DF∥AB

∴四边形DEBF是平行四边形

∵DE∥BC

∴∠EDB＝∠DBF

∵BD平分∠ABC

∴∠ABD＝∠DBF＝∠ABC

∴∠ABD＝∠EDB

∴DE＝BE

∴四边形BEDF为菱形；

(2) ∠A＝100°,∠C＝30°,

∵BD平分∠ABC

∴∠ABD＝∠DBF＝∠ABC

∵DE∥BC

∴∠EDB＝∠DBF= 25°.