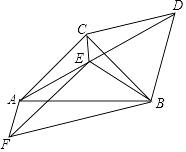
题目内容
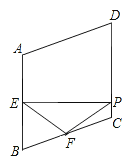
【题目】如图,正方形ABCD中,E为BC上一点,BE=2CE,连接DE,F为DE中点,以DF为直角边作等腰Rt△DFG,连接BG,将△DFG绕点D顺时针旋转得△DF′G′,G′恰好落在BG的延长线上,连接F′G,若BG=2 ![]() ,则S△GF′G′= .
,则S△GF′G′= . 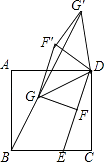
【答案】![]()
【解析】解:如图,作GM⊥BC于M,MG的延长线交AD于N,作DK⊥BG′于K,作KQ⊥DG′于Q,作F′H′BG′于H,BG′交AD于P.
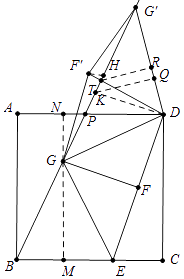
∵BE=2EC,设EC=a,则BE=2a,BC=CD=MN=3a,
∵DG=GE,∠DGE=90°,易证△DGN≌△GEM,设EM=x,
则GN=EM=x,GM=DN=CM=a+x,
∴x+x+a=3a,
∴x=a,
∴BM=EM,∵GM⊥BE,
∴GB=GE=2 ![]() ,
,
∵GM=2a.EM=a,
在Rt△GEM中,可得5a2=20,
∵a>0,
∴a=2,
∴AB=BC=CD=AD=6,GM=4,CM=DN=4,AN=GN=2,DF=EF=GF=G′F′= ![]() ,DG=GE=DG′=2
,DG=GE=DG′=2 ![]() ,
,
∵△GBM∽△BPA,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴AP=PD=3,
由△APB∽△KPD,可得DK= ![]() ,
,
∵DG′=DG,DK⊥GG′,
∴G′K=GK= ![]() =
= ![]() ,
,
设BG′交DF′于T,作TR⊥DG′于R,
∵tan∠TG′R= ![]() =
= ![]() =
= ![]() ,设TR=3k,RG′=4k,
,设TR=3k,RG′=4k,
∵∠TDR=45°,
∴TR=DR=3k,
∴7k=2 ![]() ,
,
∴k= ![]() ,
,
∴TG′=5k= ![]() ,
,
由△′F′H∽△G′TF′,
可得G′H= ![]() ,
,
在Rt△G′F′H中,F′H= ![]() =
= ![]() ,
,
∴S△GG′F′= ![]() GG′F′H=
GG′F′H= ![]() ×
× ![]() ×
× ![]() =
= ![]() ,
,
所以答案是 ![]() .
.
【考点精析】关于本题考查的等腰直角三角形和勾股定理的概念,需要了解等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能得出正确答案.