Question

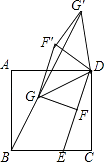
【题目】如图，已知等腰Rt△ABC，∠ACB=90°，CA=CB，以BC为边向外作等边△CBA，连接AD，过点C作∠ACB的角平分线与AD交于点E，连接BE．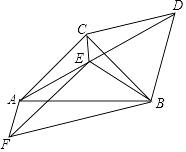

（1）若AE=2，求CE的长度；
（2）以AB为边向下作△AFB，∠AFB=60°，连接FE，求证：FA+FB= FE．

Answer 1

【答案】
（1）解：延长CE交AB于G，

∵△BAC是等腰直角三角形，CE平分∠ACB，

∴CG⊥AB，

∴∠AGC=90°，

∵CA=CB，∠ACB=90°，

∴∠CAB=45°，

∴△CAG是等腰直角三角形，

∵△BCD是等边三角形，

∴BC=CD=AC，∠BCD=60°，

∴∠CAD=∠CDA，

∴∠ACD=∠ACB+∠BCD=150°，

∴∠CAD=∠CDA=15°，

∴∠EAB=∠CAB﹣∠CAD=30°，

在Rt△AEG中，∠EAG=30°，AE=2，

∴AE= ，EG=1，

∵CG=AG= ，

∴CE=CG﹣EG= ﹣1．

（2）解：延长FB到H，使得BH=AF，连接EH．作EI⊥BF于I．

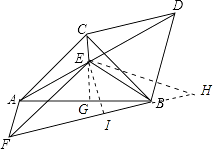
由（1）可知：AC=BC，CE平分∠ACB，

∴∠ACE=∠BCE，

∵CE=CE，

∴△ACE≌△BCE，

∴AE=BE，

∴∠EAB=∠EBC=30°，

在△AFB中，∠AFB=60°，

∴∠FAB+∠FBA=120°，

∴∠FAE=∠EAB+∠FAB=30°+∠FAB，

∠EBH=180°﹣∠EBA﹣∠ABF=150°﹣（120°﹣∠ABF）=30°+∠FAB，

∴∠EBH=∠FAE，

∴△AFE≌△BHE，

∴∠AFE=∠BHE，EF=EH，

∴∠EFB=∠EBH=∠AFE=30°，

∵EI⊥FH，

∴EI=IH，

在Rt△FEI中，∠EFI=30°，

∴FI= FE，

∴FH=BH+FB= FE，

∴FA+FB= FE．

【解析】（1）延长CE交AB于G，首先判断出△CAG是等腰直角三角形，然后找到∠EAB=∠CAB﹣∠CAD=30°，分别求出CG,EG即可解决问题；
（2）延长FB到H，使得BH=AF，连接EH．作EI⊥BF于I．由△ACE≌△BCE，推出AE=BE，推出∠EAB=∠EBC=30°，由△AFE≌△BHE，推出∠AFE=∠BHE，EF=EH，可得∠EFB=∠EBH=∠AFE=30°，又EI⊥FH，故在Rt△FEI中，∠EFI=30°，从而得出FI= FE，可得FA+FB= FE．
【考点精析】本题主要考查了等腰直角三角形和等边三角形的性质的相关知识点，需要掌握等腰直角三角形是两条直角边相等的直角三角形；等腰直角三角形的两个底角相等且等于45°；等边三角形的三个角都相等并且每个角都是60°才能正确解答此题．