题目内容
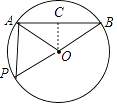
【题目】如图，已知AB是⊙O的弦，半径OA=2cm，∠AOB=120°
（1）求tan∠OAB的值；
（2）求图中阴影部分的面积S；
（3）在⊙O上一点P从A点出发，沿逆时针方向运动一周，回到点A，在点P的运动过程中，满足S△POA=S△AOB时，直接写出P点所经过的弧长（不考虑点P与点B重合的情形）．
【答案】
（1）解：∵OA=OB，
∴∠OAB=∠OBA，
∵∠OAB= 
（180°﹣120°）=30°，
∴tan∠OAB=tan30°= 
；
（2）解：作OC⊥AB于C，如图，则AC=BC，
在Rt△OAC中，OC= OA=1，AC= 
OC= ，
∴AB=2AC=2 ，
∴S弓形AB=S扇形AOB﹣S△AOB= 
﹣ 2 1=（ 
π﹣ ）cm2；
（3）解：延长BO交⊙O于P，
∵OP=OB，
∴此时S△AOP=S△AOB，
∵∠AOP=∠OAB+∠OBA=60°，
∴此时P点所经过的弧长= 
= 
π（cm）；
当点P在 
上，且∠AOP=60°时，时S△AOP=S△AOB，
此时P点所经过的弧长=2π2﹣ π= 
π（cm）；
当∠AOP=120时，S△AOP=S△AOB，
∴此时P点所经过的弧长= 
= π（cm）；
综上所述，P点所经过的弧长为 πcm或 πcm或 πcm．
【解析】（1）求角的三角函数须把此角放在直角三角形中，要过O点作垂线；（2）阴影部分面积可转化为S弓形AB=S扇形AOB﹣S△AOB；（3）先考虑P在优弧APB上或在劣弧AB上，算出圆心角，由弧长公式算出长度.
【考点精析】解答此题的关键在于理解圆周角定理的相关知识，掌握顶点在圆心上的角叫做圆心角;顶点在圆周上，且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半，以及对弧长计算公式的理解，了解若设⊙O半径为R，n°的圆心角所对的弧长为l，则l=nπr/180;注意：在应用弧长公式进行计算时，要注意公式中n的意义．n表示1°圆心角的倍数，它是不带单位的．
