题目内容
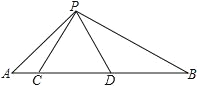
【题目】如图,点 C、D 在线段 AB 上,△PCD 是等边三角形,∠APB=120°
(1) 求证:△ACP∽△PDB
(2) 若 PC=3,AC=1,求 BD 的长
【答案】(1)见详解;(2) ![]() .
.
【解析】
(1)根据等边三角形的性质得到∠PCD=∠PDC=∠CPD=60°,于是推出∠ACP=∠PDB=120°,等量代换得到∠BPD=∠CAP,根据相似三角形的性质即可得证;
(2) 由相似三角形的性质得到![]() ,计算即可求出BD的长.
,计算即可求出BD的长.
(1) ∵△PCD是等边三角形,
∴∠PCD=∠PDC=∠CPD=60°,
∴∠ACP=∠PDB=120°,
∵∠APB=120°,
∴∠APC+∠BPD=60°,
∵∠CAP+∠APC=60°,
∴∠BPD=∠CAP,
∴△ACP∽△PDB;
(2) ∵△PCD 是等边三角形,
∴PD=PC=3,
∵△ACP∽△PDB,
∴![]() ,即
,即![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】一只不透明的袋子中装有4个质地、大小均相同的小球,这些小球分别标有数字2,3,4,x,甲、乙两人每次同时从袋中各随机摸出1个球,并计算摸出的这2个小球上数字之和,记录后都将小球放回袋中搅匀,进行重复试验,实验数据如下表:
摸球总次数 | 20 | 30 | 60 | 90 | 120 | 180 | 240 | 330 | 450 |
“和为6”出现的频数 | 10 | 13 | 24 | 30 | 37 | 58 | 82 | 110 | 150 |
“和为6”出现的频数 | 0.50 | 0.43 | 0.40 | 0.33 | 0.31 | 0.32 | 0.34 | 0.33 | 0.33 |
解答下列问题:
(1)如果实验继续进行下去,根据上表数据,出现“和为6”的频率将稳定在它的概率附近,估计出现“和为6”的概率是 .
(2)当x=5时,请用列表法或树状图法计算“和为6”的概率
(3)判断x=5是否符合(1)的结论,若符合,请说明理由,若不符合,请你写出一个符合(1)的x的值.