题目内容
【题目】综合题。
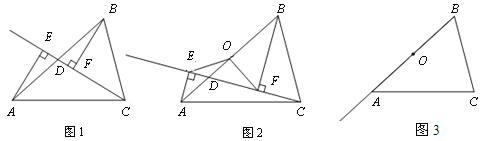
(1)如图,在△ABC中,AC=BC,∠ACB=90°,直线l过点C,分别过A、B两点作AD⊥l于点D,作BE⊥l于点E.求证:DE=AD+BE.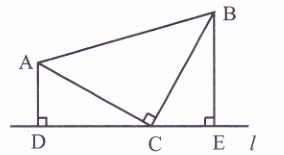
(2)如图,已知Rt△ABC,∠C=90°.用尺规作图法作出△ABC的角平分线AD;(不写作法,保留作图痕迹)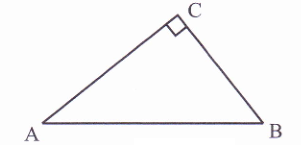
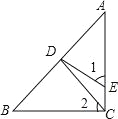
(3)若AB=10,CD=3,求△ABD的面积.
【答案】
(1)
证明:∵∠ACB=90
∴∠ACD+∠BCE=90
∵ AD⊥l
∴∠ACD+∠CAD=90
∴∠CAD=∠BCE
∵BE⊥l,AD⊥l
∴∠ADC=∠BEC=90
∵AC=BC
∴△ACD≌△CBE
∴AD=CE,CD=BE
∵DE= CD+ CE
∴DE=AD+BE.
(2)
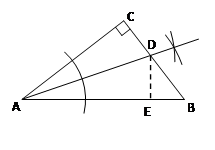
(3)
解:过点D作DE⊥AB于E

∵DC⊥AC,DE⊥AB
∴DE=DC=3
∴ ![]()
【解析】(1)根据“同角的余角相等”可证得∠CAD=∠BCE,再由AC=BC,∠ADC=∠BEC=90,可证明△ACD≌△CBE,则DE=AD+BE=CD+ CE.(2)角平分线的尺规作图方法,过A画弧交角两边的两点,再分别这两点为圆心画两条弧交于一点,连接A与这一点,交BC于点D,即AD为该角的角平分线;(3)由角平分线的性质,可作DE⊥AB于E,DE=DC=3,则可求三角形ABD的面积.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目