题目内容
【题目】在⊙O中,AB为直径,C为⊙O上一点.
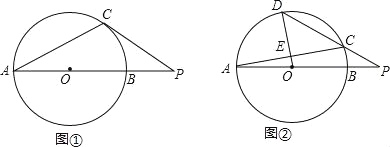
(Ⅰ)如图1.过点C作⊙O的切线,与AB的延长线相交于点P,若∠CAB=27°,求∠P的大小;
(Ⅱ)如图2,D为![]() 上一点,且OD经过AC的中点E,连接DC并延长,与AB的延长线相交于点P,若∠CAB=10°,求∠P的大小.
上一点,且OD经过AC的中点E,连接DC并延长,与AB的延长线相交于点P,若∠CAB=10°,求∠P的大小.
【答案】(Ⅰ)36°(Ⅱ)30°
【解析】
试题分析:(Ⅰ)连接OC,首先根据切线的性质得到∠OCP=90°,利用∠CAB=27°得到∠COB=2∠CAB=54°,然后利用直角三角形两锐角互余即可求得答案;
(Ⅱ)根据E为AC的中点得到OD⊥AC,从而求得∠AOE=90°﹣∠EAO=80°,然后利用圆周角定理求得∠ACD=![]() ∠AOD=40°,最后利用三角形的外角的性质求解即可.
∠AOD=40°,最后利用三角形的外角的性质求解即可.
试题解析:(Ⅰ)如图,连接OC,
∵⊙O与PC相切于点C,
∴OC⊥PC,即∠OCP=90°,
∵∠CAB=27°,
∴∠COB=2∠CAB=54°,
在Rt△AOE中,∠P+∠COP=90°,
∴∠P=90°﹣∠COP=36°;
(Ⅱ)∵E为AC的中点,
∴OD⊥AC,即∠AEO=90°,
在Rt△AOE中,由∠EAO=10°,
得∠AOE=90°﹣∠EAO=80°,
∴∠ACD=![]() ∠AOD=40°,
∠AOD=40°,
∵∠ACD是△ACP的一个外角,
∴∠P=∠ACD﹣∠A=40°﹣10°=30°.


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目