题目内容
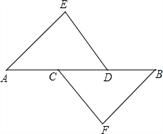
【题目】如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的中线,DE⊥AB于点D,交AC于点E.
(1)若BC=3,AC=4,求CD的长;
(2)求证:∠1=∠2.
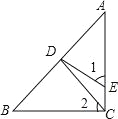
【答案】(1)2.5(2)∠1=∠2
【解析】
试题分析:(1)由勾股定理求出AB,再根据直角三角形斜边上的中线等于斜边的一半解答即可;
(2)由直角三角形的锐角关系和等腰三角形的性质即可得出结论.
试题解析:(1)解:∵∠ACB=90°,BC=3,AC=4,
∴AB=![]() =5,
=5,
∵CD是AB边上的中线,
∴CD=![]() AB=2.5;
AB=2.5;
(2)证明:∵∠ACB=90°,
∴∠A+∠B=90°,
∵DE⊥AB,
∴∠A+∠1=90°,
∴∠B=∠1,
∵CD是AB边上的中线,
∴BD=CD,
∴∠B=∠2,
∴∠1=∠2.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目