题目内容
【题目】(本小题满分9分)已知点D是![]() 边AB上一动点(不与A,B重合)分别过点A,B向直线CD作垂线,垂足分别为E,F,O为边AB的中点.
边AB上一动点(不与A,B重合)分别过点A,B向直线CD作垂线,垂足分别为E,F,O为边AB的中点.
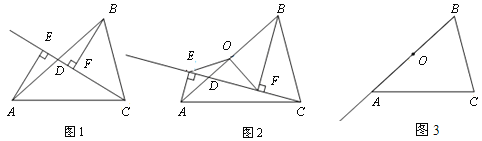
(1)如图1,当点D与点O重合时,AE与BF的位置关系是____________,OE与OF的数量关系是__________;
(2)如图2,当点D在线段AB上不与点O重合时,试判断OE与OF的数量关系,并给予证明;
(3)如图3,当点D在线段BA的延长线上时,此时(2)中的结论是否成立?请画出图形并写出主要证明思路. (备注:直角三角形中,斜边上的中线等于斜边的一半)
【答案】见解析
【解析】(1)AE∥BF,OE=OF.
如图,
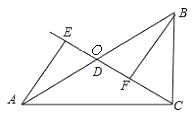
当点D与点O重合时,AE与BF的位置关系是AE∥BF,OE与OF的数量关系是OE=OF.
理由是:∵O为AB的中点,
∴AO=BO,
∵AE⊥CD,BF⊥CO,
∴AE∥BF,∠AEO=∠BFO=90°,(2分)
在![]() 和
和![]() 中
中
∠AOE=∠BOF,∠AEO=∠BFO,AO=BO,
∴△AEO≌△BFO,
∴OE=OF,
故答案为:AE∥BF,OE=OF(3分)
(2)结论:OE=OF. (4分)
证明:如图,延长EO交BF于G.
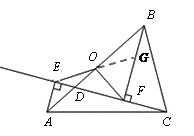
∵AE∥BF,
∴∠AEO=∠BGO,
在![]() 和
和![]() 中,
中,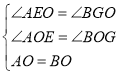 ,
,
∴△AEO≌△BGO(ASA).∴OE=OG.
∵BF⊥CD,∴FO是![]() 斜边上的中线,
斜边上的中线,
∴OE=OF=OG,
即OE=OF.(6分)
(3)(2)中的结论仍然成立. (7分)
所画图形如图所示,
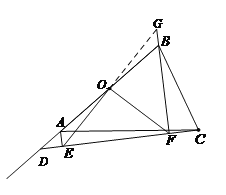 (8分)
(8分)
证明思路:延长EO、FB交于G.
由(2)的证明思路可以得到△AOE≌△BOG,由全等得到OE=OG;由BF⊥CD,得到FO是![]() 斜边GE上的中线;可得到OE=OF.(9分)
斜边GE上的中线;可得到OE=OF.(9分)

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目