题目内容
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,﹣2)和(0,﹣1)之间(不包括这两点),对称轴为直线x=1,下列结论:①abc<0;②9a+3b+c=0;③4ac﹣b2<2a;④2b=3a.
其中正确的结论是( )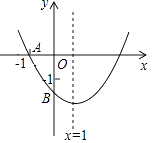
A.①③
B.②④
C.①④
D.②③
【答案】D
【解析】①∵抛物线开口向上,对称轴为直线x=1,与y轴的交点B在(0,﹣2)和(0,﹣1)之间(不包括这两点),
∴a>0,﹣ ![]() =1,c<0,
=1,c<0,
∴b=﹣2a<0,
∴abc>0,结论①错误;②∵二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),对称轴为直线x=1,
∴二次函数y=ax2+bx+c(a≠0)的图象与x轴的另一个交点为(3,0),
∴9a+3b+c=0,结论②正确;③∵二次函数y=ax2+bx+c(a≠0)的图象与y轴的交点B在(0,﹣2)和(0,﹣1)之间(不包括这两点),
∴抛物线顶点纵坐标 ![]() <﹣1,
<﹣1,
∵a>0,
∴4ac﹣b2<﹣4a<2a,结论③正确;④∵抛物线对称轴为直线x=1,
∴﹣ ![]() =1,b=﹣2a,结论④错误.
=1,b=﹣2a,结论④错误.
综上所述,正确的结论有:②③.
所以答案是:D.
【考点精析】本题主要考查了二次函数的性质和二次函数图象以及系数a、b、c的关系的相关知识点,需要掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小;二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c)才能正确解答此题.

【题目】点燃一根蜡烛后,蜡烛的高度h(厘米)与燃烧时间t(分)之间的关系如下表:
t/分 | 0 | 2 | 4 | 6 | 8 | 10 |
h/厘米 | 30 | 29 | 28 | 27 | 26 | 25 |
写出蜡烛的高度h(厘米)与燃烧时间t(分)之间的关系式_____;这根蜡烛最多能燃烧的时间为_____分.
【题目】为加快建设经济强、环境美、后劲足、群众富的实力微山,魅力微山,活力微山,幸福微山;聚力脱贫攻坚,全面完成脱贫任务,某乡镇特制定一系列帮扶甲、乙两贫困村的计划,现决定从某地运送1225箱鱼苗到甲、乙两村养殖.若用大、小货车共20辆,则恰好能一次性运完这批鱼苗,已知这两种大小货车的载货能力和其运往甲、乙两村的运费如表:
车型 | 载货能力(箱/辆) | 运费 | |
甲村(元/辆) | 乙村(元/辆) | ||
大货车 | 70 | 800 | 900 |
小货车 | 35 | 400 | 600 |
(1)求这20辆车中大、小货车各多少辆?
(2)现安排其中16辆货车前往甲村,其余货车前往乙村,设前往甲村的大货车为x辆,前往甲、乙两村总费用为y元,试求出y与x的函数解析式及x的取值范围;
(3)在(2)的条件下,若运往甲村的鱼苗不少于980箱,请你写出使总费用最少的货车调配方案,并求出最少费用.