题目内容
【题目】如图,抛物线y=-x2+5x+n与x轴交于点A(1,0)和点C,与y轴交于点B.
(1)求抛物线的解析式;
(2)求△ABC的面积;
(3)P是y轴上一点,且△PAB是以AB为腰的等腰三角形,试求点P的坐标.
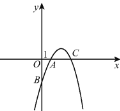
【答案】(1) y=-x2+5x-4 ;(2)6;(3) P的坐标为(0,![]() -4)或(0,-
-4)或(0,-![]() -4)或(0,4).
-4)或(0,4).
【解析】
(1)将点A的坐标代入抛物线中,即可得出二次函数的解析式;(2)求得点B、C的坐标,根据三角形的面积公式求解即可;(3)分PB=AB和PA=AB两种情况求点P的坐标即可.
解:(1)根据题意,得0=-1+5+n,解得n=-4,
∴抛物线的解析式为y=-x2+5x-4.
(2)令y=0,即-x2+5x-4=0,解得x1=1,x2=4,
∴点C坐标为(4,0).
令x=0,解得y=-4,∴点B的坐标为(0,-4).
∴由图象可得S△ABC=![]() ×OB×AC=
×OB×AC=![]() ×4×3=6.
×4×3=6.
(3)①当PA=AB时,则点O为PB的中点,
∴OP=OB=4,
∴点P的坐标为(0,4);
②当AB=BP时,AB=![]() ,
,
∴OP=![]() ±4,∴点P的坐标为(0,
±4,∴点P的坐标为(0,![]() -4)或(0,-
-4)或(0,-![]() -4).
-4).
综上,点P的坐标为(0,![]() -4)或(0,-
-4)或(0,-![]() -4)或(0,4).
-4)或(0,4).

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目