题目内容
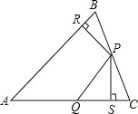
【题目】如图,△ABC中,∠ACB>90°,AE平分∠BAC,AD⊥BC交BC的延长线于点D.
(1)若∠B=30°,∠ACB=100°,求∠EAD的度数;
(2)若∠B=α,∠ACB=β,试用含α、β的式子表示∠EAD.
【答案】(1)![]() ,(2)
,(2)![]() .
.
【解析】
(1)根据垂直的定义得到∠D=90°,根据邻补角的定义得到∠ACD![]() ,根据三角形的内角和得到∠BAC=50°,根据角平分线的定义得到∠CAE
,根据三角形的内角和得到∠BAC=50°,根据角平分线的定义得到∠CAE![]() ∠BAC=25°,于是得到结论; (2)根据垂直的定义得到∠D=90°,得到∠ACD=
∠BAC=25°,于是得到结论; (2)根据垂直的定义得到∠D=90°,得到∠ACD=![]() ,求得∠BAC
,求得∠BAC![]() ,根据角平分线的定义得到∠CAE
,根据角平分线的定义得到∠CAE![]() ∠BAC
∠BAC![]() ,根据角的和差即可得到结论.
,根据角的和差即可得到结论.
解:(1)∵AD⊥BC, ∴∠D=90°,
∵∠ACB=100°, ∴∠ACD![]() ,
,
∴∠CAD=![]() , ∵∠B=30°,
, ∵∠B=30°,
∴∠BAD![]() , ∴∠BAC=50°,
, ∴∠BAC=50°,
∵AE平分∠BAC, ∴∠CAE![]() ∠BAC=25°,
∠BAC=25°,
∴∠EAD=∠CAE+∠CAD=35°;
(2)∵AD⊥BC, ∴∠D=90°,
∵∠ACB=β, ∴∠ACD=![]() ,
,
∴∠CAD![]() ,
,
∵∠B=α, ∴∠BAD=![]() ,
,
∴∠BAC![]() ,
,
∵AE平分∠BAC, ∴∠CAE![]() ∠BAC
∠BAC![]() ,
,
∴∠EAD=∠CAE+∠CAD=![]() .
.

练习册系列答案
相关题目