题目内容
【题目】如图,抛物线y=ax2+2ax+c的图象与x轴交于A、B两点(点A在点B的左边)AB=4,与y轴交于点C,OC=OA,点D为抛物线的顶点.
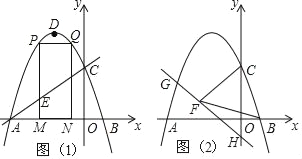
(1)求抛物线的解析式;
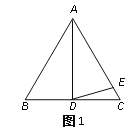
(2)点M(m,0)为线段AB上一点(点M不与点A、B重合),过点M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过点P作PQ∥AB交抛物线于点Q,过点Q作QN⊥x轴于点N,可得矩形PQNM,如图1,点P在点Q左边,当矩形PQNM的周长最大时,求m的值,并求出此时的△AEM的面积;
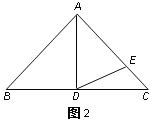
(3)已知H(0,﹣1),点G在抛物线上,连HG,直线HG⊥CF,垂足为F,若BF=BC,求点G的坐标.
【答案】(1)y=﹣x2﹣2x+3; (2)m=﹣2, ![]() ;
;
(3)点G的坐标为(![]() ,
, ![]() )或(
)或(![]() ,
, ![]() ).
).
【解析】试题分析:(1)根据抛物线y=ax2+2ax+c,可得C(0,c),对称轴为x﹣1,再根据OC=OA,AB=4,可得A(﹣3,0),最后代入抛物线y=ax2+2ax+3,得抛物线的解析式为y=﹣x2﹣2x+3;
(2)根据点M(m,0),可得矩形PQNM中,P(m,﹣m2﹣2m+3),Q(﹣2﹣m,﹣m2﹣2m+3),再根据矩形PQNM的周长=2(PM+PQ)=﹣2(m+2)2+10,可得当m=﹣2时,矩形PQNM的周长有最大值10,M的坐标为(﹣2,0),最后由直线AC为y=x+3,AM=1,求得E(﹣2,1),ME=1,据此求得△AEM的面积;
(3)连接CB并延长,交直线HG与Q,根据已知条件证明BC=BF=BQ,再根据C(0,3),B(1,0),得出Q(2,﹣3),根据H(0,﹣1),求得QH的解析式为y=﹣x﹣1,最后解方程组![]() ,可得点G的坐标.
,可得点G的坐标.
试题解析:(1)由抛物线y=ax2+2ax+c,可得C(0,c),对称轴为x=﹣![]() =﹣1,
=﹣1,
∵OC=OA,
∴A(﹣c,0),B(﹣2+c,0),
∵AB=4,
∴﹣2+c﹣(﹣c)=4,
∴c=3,
∴A(﹣3,0),
代入抛物线y=ax2+2ax+3,得
0=9a﹣6a+3,
解得a=﹣1,
∴抛物线的解析式为y=﹣x2﹣2x+3;
(2)如图1,
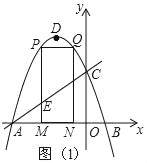
∵M(m,0),PM⊥x轴,
∴P(m,﹣m2﹣2m+3),
又∵对称轴为x=﹣1,PQ∥AB,
∴Q(﹣2﹣m,﹣m2﹣2m+3),
又∵QN⊥x轴,
∴矩形PQNM的周长
=2(PM+PQ)
=2[(﹣m2﹣2m+3)+(﹣2﹣m﹣m)]
=2(﹣m2﹣4m+1)
=﹣2(m+2)2+10,
∴当m=﹣2时,矩形PQNM的周长有最大值10,
此时,M(﹣2,0),
由A(﹣3,0),C(0,3),可得
直线AC为y=x+3,AM=1,
∴当x=﹣2时,y=1,即E(﹣2,1),ME=1,
∴△AEM的面积=![]() ×AM×ME=
×AM×ME=![]() ×1×1=
×1×1=![]() ;
;
(3)如图2,连接CB并延长,交直线HG与Q,
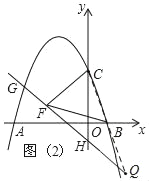
∵HG⊥CF,BC=BF,
∴∠BFC+∠BFQ=∠BCF+∠Q=90°,∠BFC=∠BCF,
∴∠BFQ=∠Q,
∴BC=BF=BQ,
又∵C(0,3),B(1,0),
∴Q(2,﹣3),
又∵H(0,﹣1),
∴QH的解析式为y=﹣x﹣1,
解方程组![]() ,可得
,可得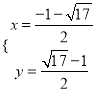 或
或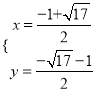 ,
,
∴点G的坐标为(![]() ,
, ![]() )或(
)或(![]() ,
, ![]() ).
).