题目内容
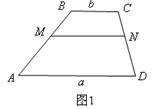
如图,在正方形ABCD中,点M是对角线BD上的一点,过点M作ME∥CD交BC于点E,作MF∥BC交CD于点F.求证:AM=EF.
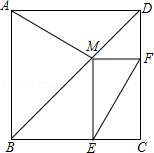

证明:过M点作MQ⊥AD,垂足为Q,作MP垂足AB,垂足为P,

∵四边形ABCD是正方形,
∴四边形MFDQ和四边形PBEM是正方形,四边形APMQ是矩形。
∴AP=QM=DF=MF,PM=PB=ME,
∵在△APM和△FME中, ,
,
∴△APM≌△FME(SAS)。
∴AM=EF。

∵四边形ABCD是正方形,
∴四边形MFDQ和四边形PBEM是正方形,四边形APMQ是矩形。
∴AP=QM=DF=MF,PM=PB=ME,
∵在△APM和△FME中,
 ,
,∴△APM≌△FME(SAS)。
∴AM=EF。
试题分析:过M点作MQ⊥AD,垂足为Q,作MP垂足AB,垂足为P,根据题干条件证明出AP=MF,PM=ME,进而证明△APM≌△FME,即可证明出AM=EF。

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
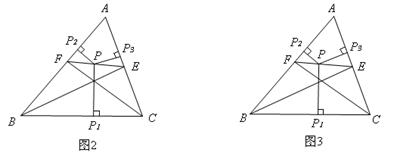
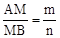 ,则有结论:
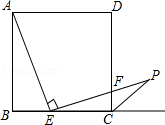
,则有结论: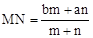 。
。
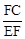 的值为 ;
的值为 ; ADCE中,DE最小的值是
ADCE中,DE最小的值是
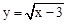 的自变量x的取值范围是x>3
的自变量x的取值范围是x>3 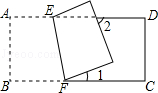
 .
.