题目内容
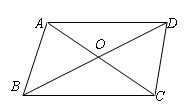
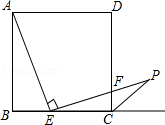
如图,在边长为3的正方形ABCD中,点E是BC边上的点,BE=1,∠AEP=90°,且EP交正方形外角的平分线CP于点P,交边CD于点F,
(1)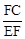 的值为 ;
的值为 ;
(2)求证:AE=EP;
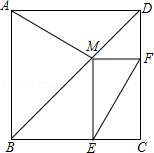
(3)在AB边上是否存在点M,使得四边形DMEP是平行四边形?若存在,请给予证明;若不存在,请说明理由.

(1)
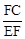 的值为 ;
的值为 ;(2)求证:AE=EP;
(3)在AB边上是否存在点M,使得四边形DMEP是平行四边形?若存在,请给予证明;若不存在,请说明理由.
解:(1)∵四边形ABCD是正方形,∴∠B=∠D。
∵∠AEP=90°,∴∠BAE=∠FEC。
在Rt△ABE中,AB=3,BE=1,∴ 。
。
∴ ,
,
(2)证明:在BA边上截取BG=BE,连接GE,

∵∠B=90°,BG=BE,∴∠BGE=45°。∴∠AGE=135°。
∵CP平分外角,∴∠DCP=45°。∴∠ECP=135°。
∴∠AGE=∠ECP。
∵AB=CB,BG=BE,
∴AB﹣BG=BC﹣BE,即:AG=CE。
又∠GAE=∠CEP,
∵在△AGE和△ECP中,∠AGE=∠ECP,AG=CE,∠GAE=∠CEP,
∴△AGE≌△ECP(ASA)。
∴AE=EP。
(3)存在。证明如下:
如图,作DM⊥AE于AB交于点M,则有:DM∥EP,

连接ME、DP,
∵在△ADM与△BAE中,
AD=BA,∠ADM=∠BAE,∠DAM=∠ABE,
∴△ADM≌△BAE(AAS)。∴MD=AE。
∵由(2)AE=EP,∴MD=EP。∴MD EP。
EP。
∴四边形DMEP为平行四边形。
∵∠AEP=90°,∴∠BAE=∠FEC。
在Rt△ABE中,AB=3,BE=1,∴
 。
。∴
 ,
,(2)证明:在BA边上截取BG=BE,连接GE,

∵∠B=90°,BG=BE,∴∠BGE=45°。∴∠AGE=135°。
∵CP平分外角,∴∠DCP=45°。∴∠ECP=135°。
∴∠AGE=∠ECP。
∵AB=CB,BG=BE,
∴AB﹣BG=BC﹣BE,即:AG=CE。
又∠GAE=∠CEP,
∵在△AGE和△ECP中,∠AGE=∠ECP,AG=CE,∠GAE=∠CEP,
∴△AGE≌△ECP(ASA)。
∴AE=EP。
(3)存在。证明如下:
如图,作DM⊥AE于AB交于点M,则有:DM∥EP,

连接ME、DP,
∵在△ADM与△BAE中,
AD=BA,∠ADM=∠BAE,∠DAM=∠ABE,
∴△ADM≌△BAE(AAS)。∴MD=AE。
∵由(2)AE=EP,∴MD=EP。∴MD
 EP。
EP。∴四边形DMEP为平行四边形。
试题分析:(1)由正方形的性质可得:∠B=∠C=90°,由同角的余角相等,可证得:∠BAE=∠CEF,根据同角的正弦值相等即可解答:
(2)在BA边上截取BG=BE,连接GE,根据角角之间的关系得到∠AGE=∠ECP,由AB=CB,BG=BE,得AG=EC,结合∠GAE=∠CEP,证明△AKE≌△ECP,于是结论得出。
(3)作DM⊥AE于AB交于点M,连接ME、DP,易得出DM∥EP,由已知条件证明△ADM≌△BAE,进而证明MD=EP,四边形DMEP是平行四边形即可证出。

练习册系列答案
相关题目