题目内容
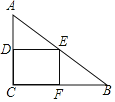
【题目】如图,在RT△ABC中,∠ACB=90°,AC=6,BC=8,矩形CDEF的顶点E为AB的中点,D,F两点分别在边AC,BC上,且![]() ,将矩形CDEF以每秒1个单位长度的速度沿射线CB方向匀速运动,当点C与点B重合时停止运动,设运动时间为t秒,矩形CDEF与△ABC重叠部分的面积为S,则反映S与t的函数关系的图象为( )
,将矩形CDEF以每秒1个单位长度的速度沿射线CB方向匀速运动,当点C与点B重合时停止运动,设运动时间为t秒,矩形CDEF与△ABC重叠部分的面积为S,则反映S与t的函数关系的图象为( )
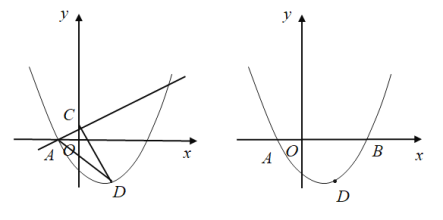
A.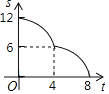 B.
B.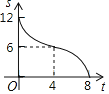
C.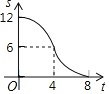 D.
D.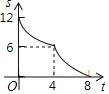
【答案】C
【解析】
证明△DEF≌△BFE(AAS),则DE=FB=CF=![]() BC=4;分0≤t≤4、4<t≤8两种情况,分别求出函数表达式,即可求解.
BC=4;分0≤t≤4、4<t≤8两种情况,分别求出函数表达式,即可求解.
解:如图1,连接DF,
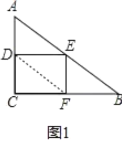
∵![]() ,即tanB=tan∠EDF,
,即tanB=tan∠EDF,
∴∠B=∠EDF,而∠DEF=∠EFB=90°,EF=EF,
∴△DEF≌△BFE(AAS),
∴DE=FB=CF=![]() BC=4,即点F是BC的中点,
BC=4,即点F是BC的中点,
EF=FBtanB=4×![]() =3,
=3,
故矩形DCFE的面积为3×4=12;
当0≤t≤4时,如图2,
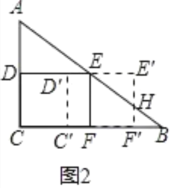
设直线AB交D′C′F′E′于点H,
则EE′=t,HE′=EE′tan∠E′EH=EE′tanB=![]() t,
t,
S=S矩形D′C′F′E′S△E′EH=12![]() ×t×
×t×![]() t=12
t=12![]() ,
,
该函数为开口向下的抛物线,当t=4时,S=6;
当4<t≤8时,
同理可得:S=![]() ,
,
该函数为开口向上的抛物线;
故选:C.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目