题目内容
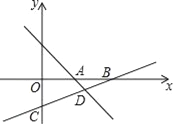
【题目】如图,在平面直角坐标系中,一次函数y1=ax+b(a≠0)的图象与反比例函数y2=![]() (k≠0)的图象交于A、B两点,与x轴交于点C,过点A作AH⊥x轴于点H,点O是线段CH的中点,AC=4
(k≠0)的图象交于A、B两点,与x轴交于点C,过点A作AH⊥x轴于点H,点O是线段CH的中点,AC=4![]() ,cos∠ACH=
,cos∠ACH=![]() .
.
(1)求该反比例函数和一次函数的解析式;
(2)在x轴上是否存在点P,使三角形PAC是等腰三角形?若存在,请求出P点坐标;不存在,请说明理由.

【答案】(1)反比例函数的解析式为:y2=﹣![]() ,一次函数解析式为y1=﹣2x+4;(2)P点坐标为(﹣8,0).
,一次函数解析式为y1=﹣2x+4;(2)P点坐标为(﹣8,0).
【解析】分析:(1)解直角△ACH求得CH与AH,即可得点A的坐标;由点A,C的坐标,用待定系数法求直线AB的解析式;(2)因为点A,C确定,点P在x轴上,所以设P(m,0),分三种情况求解,①顶点是点A时,②顶点是点C时,③顶点是点P时.
详解:(1)∵AC=![]() ,cos∠ACH=
,cos∠ACH=![]() ,∴
,∴![]() ,
,
解得CH=4,
由勾股定理得,AH=![]() =8,
=8,
∵点O是线段CH的中点,
∴点A的坐标为(﹣2,8),点C的坐标为(2,0),
∴反比例函数的解析式为:y2=﹣![]() ,
,
由点A,C的坐标列方程组![]() ,
,
解得,![]() ,
,
∴一次函数解析式为y1=﹣2x+4;
(2)设P点坐标为(m,0),
①当点A为等腰三角形的顶点时,PH=CH=4,则OP=6,
∴P点坐标为(﹣6,0);
②当点C为等腰三角形的顶点时,PC=CA=![]() ,
,
则OP=![]() +2或
+2或![]() ﹣2,
﹣2,
∴P点坐标为(2﹣![]() ,0)或(
,0)或(![]() +2,0);
+2,0);
③当点P为顶点时,点P为AC垂直平分线与x轴的交点,PA=PC,
则(2﹣m)2=(﹣2﹣m)2+82,
解得,m=﹣8,
∴P点坐标为(﹣8,0).,

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目