题目内容
【题目】如图,已知⊙O的半径为6cm,射线PM经过点O,OP=10cm,射线PN与⊙O相切于点Q.A、B两点同时从点P出发,点A以5cm/s的速度沿射线PM方向运动,点B以4cm/s的速度沿射线PN方向运动,设运动时间为t s. 
(1)求PQ的长;
(2)当直线AB与⊙O相切时,求证:AB⊥PN;
(3)当t为何值时,直线AB与⊙O相切?
【答案】
(1)解:如图1中,连接OQ,
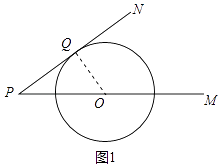
∵PN与⊙O相切于点Q,
∴OQ⊥PN,
∴∠OQP=90°,
∵OQ=6cm,OP=10cm,
∴PQ= ![]() =
= ![]() =8
=8
(2)解:如图2中,过点O作OC⊥AB于C.
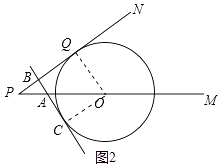
由题意,PA=5t,PB=4t,
∵OP=10,PQ=8,
∴ ![]() =
= ![]() ,∵∠P=∠P,
,∵∠P=∠P,
∴△PBA∽△PQO,
∴∠PBA=∠PQO=90°,
∴AB⊥PN
(3)解:∵∠BQO=∠CBQ=∠OCB=90°,
∴四边形OCBQ是矩形,
∴BQ=OC=6,
∵OC=6cm,
∴BQ=6cm.
①当AB运动到图2位置时,BQ=PQ﹣PB=6,
∴8﹣4t=6,
∴t=0.5s,
②当AB运动到图3位置时,

BQ=AB﹣PQ=6,
∴4t﹣8=6,
∴t=3.5s,
综上所述,t=0.5s或3.5s时,直线AB与⊙O相切
【解析】(1)连接OQ,在Rt△OPQ中,利用勾股定理即可解决问题.(2)如图2中,过点O作OC⊥AB于C.只要证明△PBA∽△PQO,即可推出∠PBA=∠PQO=90°.(3)首先证明四边形OCBQ是矩形,分两种情形列出方程即可解决问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目