Question

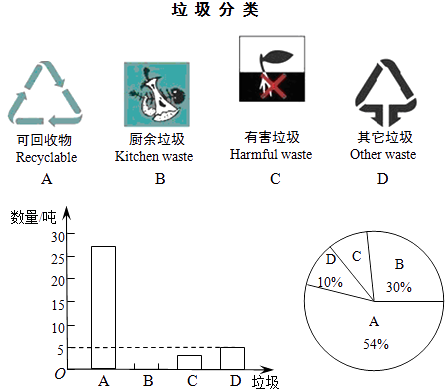
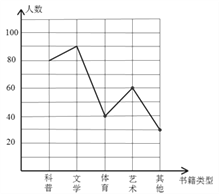
【题目】学校准备在各班设立图书角以丰富同学们的课余文化生活，为了更合理的搭配各类书籍，学校团委以“我最喜爱的书籍”为主题，对学生最喜爱的一种书籍类型进行随机抽样调查，收集整理数据后，绘制出以下两幅未完成的统计图，请根据图1和图2提供的信息，解答下列问题：

（1）在这次抽样调查中，一共调查了多少名学生？

（2）请把折线统计图（图1）补充完整；

（3）求出扇形统计图（图2）中，体育部分所对应的圆心角的度数；

（4）如果这所中学共有学生1800名，那么请你估计最喜爱科普类书籍的学生人数．

（5）学校若在喜爱艺术、文学、科普、体育四类中任意抽取两类建立兴趣小组，求出恰好选中是体育和科普两类的概率？

Answer 1

【答案】（1）300人. （2）补图见解析;（3）; （4）480人;（5）.

【解析】试题分析：

（1）由折线图知喜爱文学的人数，由扇形统计图可知喜爱文学学生所占的百分比，则此则可求出参加调查学生的总数；

（2）结合折线图与扇形图计算出喜爱艺术的人数和其他的人数；

（3）用喜爱体育学生点总人数的百分比乘以360°；

（4）用样本估计总体，通过300个中喜爱科普类书籍估计结果；

（5）这是一个等可能事件，画出树状图，列出所有可能的结果，是科普和体育的结果，从而计算出是体育和科普两类的概率.

试题解析：

（1）调查的学生人数为：90÷30%=300人.

（2）如图

（3）喜爱体育书籍的学生人数为： 300―80―90―60―30＝40.

体育部分所对的圆心角为： .

（4）在抽样调查中，喜欢科普类书籍所占比例为： ，可以估计，在全校同学中，喜欢科普类书籍的人数大约占了， 人数约为1800×=480人.

（5）画出树状图：

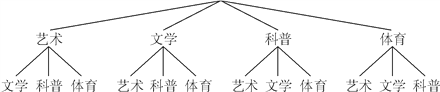
∴P(选中恰是体育和科普)＝.