题目内容
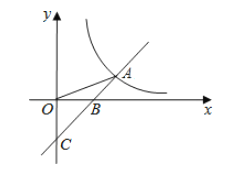
【题目】如图，在平面直角坐标系中，矩形ABCO的边CO、OA分别在x轴的负半轴、y轴的正半轴上，点D在边BC上，将该矩形沿AD折叠，点B恰好落在边OC上的E处，且△CDE为等腰直角三角形，若OA＝4，则点D的坐标是_____．
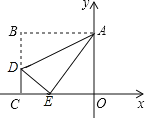
【答案】（﹣4
，
）．
【解析】
由题意根据勾股定理以及折叠的性质，即可得到CO和CD的长，进而即可得到点D的坐标．
解：由折叠可得，∠B＝∠AED＝90°，
∵△CDE是等腰直角三角形，
∴∠DEC＝45°，
∴∠AEO＝45°，
又∵∠AOE＝90°，
∴∠EAO＝∠AEO，
∴AO＝EO＝4，
∴AE＝
，
由折叠可得，AB＝AE＝，
∵四边形ABCO的矩形，
∴CO＝，
∴CE＝CO﹣EO＝，
∴CD＝，
∵点D在第二象限，
∴D（﹣，），
故答案为：（﹣4，）．
时刻准备着暑假作业原子能出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
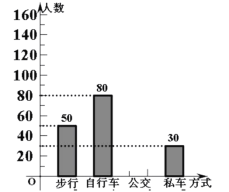
假期作业暑假成长乐园新疆青少年出版社系列答案【题目】某学校八年级共400名学生，为了解该年级学生的视力情况，从中随机抽取40名学生的视力数据作为样本，数据统计如下：
4.2 4.1 4.7 4.1 4.3 4.3 4.4 4.6 4.1 5.2
5.2 4.5 5.0 4.5 4.3 4.4 4.8 5.3 4.5 5.2
4.4 4.2 4.3 5.3 4.9 5.2 4.9 4.8 4.6 5.1
4.2 4.4 4.5 4.1 4.5 5.1 4.4 5.0 5.2 5.3
根据数据绘制了如下的表格和统计图：
等级 | 视力（x） | 频数 | 频率 |
|
| 4 | 0.1 |
|
| 12 | 0.3 |
|
|
| |
|
|
| |
| 10 | 0.25 | |
合计 | 40 | 1 | |
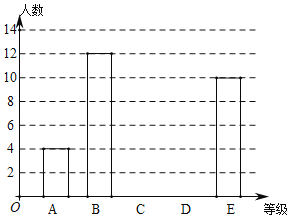
根据上面提供的信息，回答下列问题：
（1）统计表中的
，
；
（2）请补全条形统计图；
（3）根据抽样调查结果，请估计该校八年级学生视力为“
级”的有多少人？
（4）该年级学生会宣传部有2名男生和2名女生，现从中随机挑选2名同学参加“防控近视，爱眼护眼”宣传活动，请用树状图法或列表法求出恰好选中“1男1女”的概率．
