题目内容
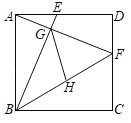
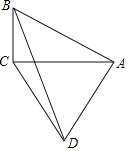
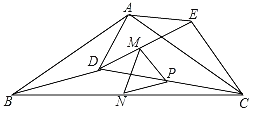
【题目】已知,△ABC和△ADE均为等腰三角形,AB=AC=5,AD=AE=2,且∠BAC=∠DAE=120°,把△ADE绕点A在平面内自由旋转.如图,连接BD,CD,CE,点M,P,N分别为DE,DC,BC的中点,连接MP,PN,MN,则△PMN的面积最大值为_____.
【答案】![]() .
.
【解析】
如图,先证明△ABD≌△ACE得到∠1=∠2,BD=CE,再根据三角形中位线的性质得到MP= ![]() CE,MP∥CE,PN∥BD,PN=
CE,MP∥CE,PN∥BD,PN= ![]() BD,则PM=PN,接着证明∠MPD=∠1+∠3,∠DPN=∠6+∠4,则∠MPN=∠ABC+∠ACB=60°,则可判断△PMN为等边三角形,所以S△PMN=
BD,则PM=PN,接着证明∠MPD=∠1+∠3,∠DPN=∠6+∠4,则∠MPN=∠ABC+∠ACB=60°,则可判断△PMN为等边三角形,所以S△PMN= ![]() ,利用三角形三边的关系得BD≤AB+AD(当且仅当B、A、D共线时取等号),然后利用BD的最大值为5得到S△PMN的最大值.
,利用三角形三边的关系得BD≤AB+AD(当且仅当B、A、D共线时取等号),然后利用BD的最大值为5得到S△PMN的最大值.
解:如图,
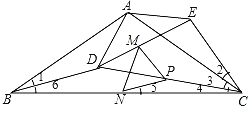
∵∠BAC=∠DAE=120°,
∴∠BAD=∠CAE,
∵AB=AC,AD=AE,
∴△ABD≌△ACE(SAS),
∴∠1=∠2,BD=CE,
∵点M,P,N分别为DE,DC,BC的中点,
∴PM为△DEC的中位线,PN为△CBD的中位线,
∴MP=![]() CE,MP∥CE,PN∥BD,PN=
CE,MP∥CE,PN∥BD,PN=![]() BD,
BD,
∴PM=PN,
∵PM∥CE,
∴∠MPD=∠2+∠3=∠1+∠3,
∵PN∥BD,
∴∠5=∠6,
∵∠DPN=∠4+∠5=∠6+∠4,
∴∠MPN=∠MPD+∠DPN=∠1+∠3+∠6+∠4=∠ABC+∠ACB=180°﹣120°=60°,
∴△PMN为等边三角形,
∴S△PMN=![]() =
=![]() ×(
×(![]() BD)2=
BD)2=![]() BD2,
BD2,
当BD最大时,S△PMN的值最大,
而BD≤AB+AD(当且仅当B、A、D共线时取等号),
∴BD的最大值为5+2=7,
∴S△PMN的最大值为![]() .
.
故答案为![]() .
.

练习册系列答案
相关题目