题目内容
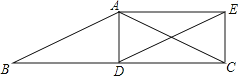
【题目】如图①，点P为∠MON的平分线上一点，以P点为顶点的角的两边分别与射线OM，ON交于A，B两点，如果∠APB绕点P旋转时始终满足OA·OB＝OP2，我们就把∠APB叫作∠MON的智慧角．
(1)如图②，已知∠MON＝90°，点P为∠MON的平分线上一点，以点P为顶点的角的两边分别与射线OM，ON交于A，B两点，且∠APB＝135°，求证：∠APB是∠MON的智慧角；
(2)如图①，已知∠MON＝α(0°＜α＜90°)，OP＝2，若∠APB是∠MON的智慧角，连接AB，用含α的式子分别表示∠APB的度数和△AOB的面积．
【答案】（1）详见解析；（2）∠APB＝180°－
,S△AOB＝2sinα..
【解析】试题分析：
(1) 在△OAP中利用三角形内角和可以求得∠OAP+∠APO为135°，再根据已知条件容易得到∠OAP=∠OPB. 由“两组内角对应相等”不难证明△AOP∽△POB. 利用相似三角形的性质可以证明OA·OB=OP2. 由于上述证明过程中所用到的几何关系不随旋转而改变，所以可以证明本小题的结论.
(2) 利用已知条件不难通过“两组对应边的比相等且夹角相等”证明△AOP∽△POB. 通过∠OAP=∠OPB可以将∠APB转化为△OAP的两个内角之和，从而利用三角形内角和获得∠APB与α的关系. 至于△AOB的面积，可以作出OB边上的高，利用锐角三角函数将这条高的长度用含有OA和α的式子表示出来. 通过三角形面积公式和OA·OB=OP2的关系可以得到△AOB的面积与α的关系.
试题解析：
(1) 证明：∵∠MON=90°，点P为∠MON平分线上的一点，
∴
，
∵在△OAP中，∠AOP+∠OAP+∠APO=180°，
∴∠OAP+∠APO=180°-∠AOP=180°-45°=135°.
∵∠APB=135°，
∴∠APO+∠OPB=135°，
∴∠OAP=∠OPB，
∵∠OAP=∠OPB，∠AOP=∠POB=45°，
∴△AOP∽△POB，
∴
，
∴OP2=OA·OB，
∴∠APB是∠MON的智慧角.
(2) 下面求解∠APB的度数.
∵∠APB是∠MON的智慧角，
∴OA·OB=OP2，
∴，
∵点P为∠MON平分线上的一点，∠MON=α (0°<α<90°)，
∴
.
∵，∠AOP=∠POB，
∴△AOP∽△POB，
∴∠OAP=∠OPB，
∵在△OAP中，∠AOP+∠OAP+∠APO=180°，
∴∠OAP+∠APO=180°-∠AOP=
，
∵∠APB=∠OPB+∠APO=∠OAP+∠APO，
∴
.
下面求解△AOB的面积.
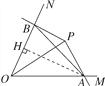
如图，过点A作AH⊥OB，垂足为H. (以下用符号S△AOB代指△AOB的面积)
∵∠MON=α (0°<α<90°)，即∠AOH=α，
∴在Rt△OHA中，
，
∴
，
∵∠APB是∠MON的智慧角，
∴OA·OB=OP2，
∴
，
∵OP=2，
∴
，即△AOB的面积为
.
