题目内容
【题目】已知BE平分∠ABD,DE平分∠BDC,且∠BED =∠ABE +∠EDC.
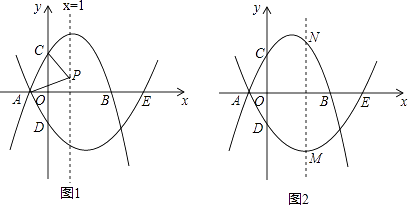
(1)如图1,求证:AB//CD;
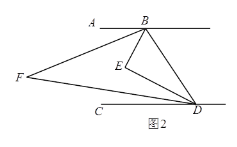
(2)如图2,若∠ABE=3∠ABF,且∠BFD=30°时,试求![]() 的值;
的值;
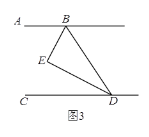
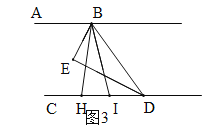
(3)如图3,若H是直线CD上一动点(不与D重合),BI平分∠HBD,画出图形,并探究出∠EBI与∠BHD的数量关系.
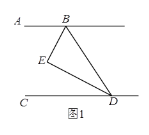
【答案】(1)证明见解析;(2)![]() ;(3)∠BHD=2∠EBI或∠BHD+2∠EBI=180°.
;(3)∠BHD=2∠EBI或∠BHD+2∠EBI=180°.
【解析】
(1)由∠BED =∠ABE +∠EDC和三角形内角和定理即可得到∠ABD+∠BDC=180°,再由同旁内角互补,两直线平行即可得到结论;
(2)由角平分线定义和∠ABD+∠BDC=180°,得到∠BED=∠ABE+∠EDC=90°.
设∠ABF=α,则∠ABE=3α,过F作FG∥AB,则有∠ABF+∠CDF=∠BFD,得到∠CDF=30°-α.过E作EH∥AB,同理可得:∠CDE=90°-3α,根据角的和差得到∠FDE=60°-2α,即可得到结论;
(3)分两种情况讨论:①当H在点D的左边时,②当H在点D右边时.
(1)∵∠BED =∠ABE +∠EDC,∠EBD+∠BED+∠BDE=180°,∴∠ABD+∠BDC=180°,∴AB∥CD;
(2)∵BE平分∠ABD,DE平分∠BDC,∴∠ABE=∠EBD,∠EDC=∠EDB.
∵∠ABD+∠BDC=180°,∴∠BED=∠ABE+∠EDC=90°.
设∠ABF=α,则∠ABE=3α.
过F作FG∥AB,则有:∠ABF+∠CDF=∠BFD,∴∠CDF=30°-α.
过E作EH∥AB,则有:∠ABE+∠CDE=∠BED,∴∠CDE=90°-3α,∴∠FDE=60°-2α,∴![]() .
.
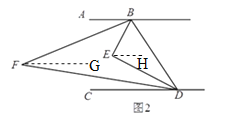
(3)分两种情况讨论:
①当H在点D的左边时,如图3.
设∠HBI=∠DBI=x,∠EBH=y,则∠EBD=2x+y,∴∠ABE=∠EBD=2x+y.
∵AB∥CD,∴∠BHD=∠ABH=2x+y+y=2(x+y)=2∠EBI;
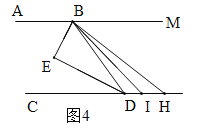
②当H在点D右边时,如图4.
设∠HBI=∠DBI=x,∠EBD=y,则∠EBI=x+y,∴∠ABH=2x+2y.
∵AB∥CD,∴∠ABH+∠BHD=180°,∴2x+2y+∠BHD=180°,∴∠BHD+2∠EBI=180°.
综上所述:∠BHD=2∠EBI或∠BHD+2∠EBI=180° .

 小学教材完全解读系列答案
小学教材完全解读系列答案