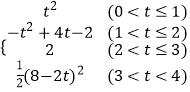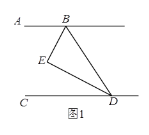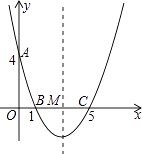题目内容
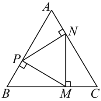
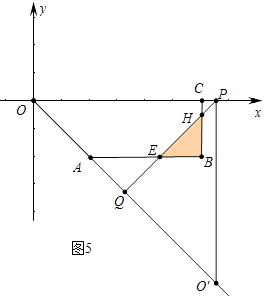
【题目】已知：如图，在四边形OABC中，AB∥OC，BC⊥x轴于点C，A（2，﹣2），B（6，﹣2），动点P从点O出发，沿着x轴正方向以每秒2个单位的速度移动，过点P作PQ垂直于直线OA，垂足为点Q，设点P移动的时间t秒（0＜t＜4）．△OPQ与四边形OABC重叠部分的面积为S．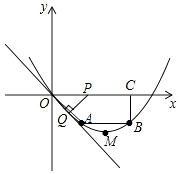
（1）求经过O、A、B三点的抛物线的解析式；
（2）若将△OPQ沿着直线PQ翻折得到△O′PQ，则当t=时，点O′恰好在抛物线上．
（3）在（2）的条件下，记△O′PQ与四边形OABC重叠的面积为S，求S与t的函数关系式，并注明自变量的取值范围．
【答案】
（1）解：设抛物线的解析式为y=ax2+bx+c，
把O（0，0），A（2，﹣2），B（6，﹣2）代入得：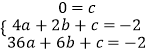 
，
解得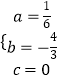 
，
所以抛物线的解析式为： 
．
（2）1
（3）解：解：由题意A（2，﹣2），可知直线OA是第二四象限的角平分线，∠AOC=45°，PQ⊥OA，△OPQ与△O′PQ是全等的等腰直角三角形，OP=PO′=2t，PQ= 
①：如图2中，当0＜t≤1时，重叠部分是△PQO′．
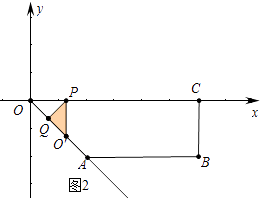
s=t2（0＜t≤1）
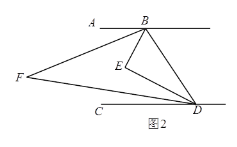
②：如图3中，当1＜t≤2时，重叠部分是四边形PQAH．
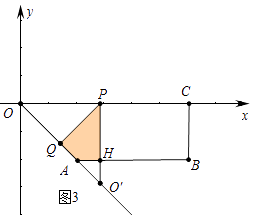
s= 
t t﹣ （2t﹣2）2=﹣t2+4t﹣2（1＜t≤2）
③：如图4中，当2＜t≤3时，重叠部分是△PEH．
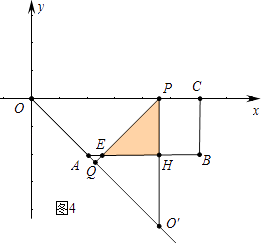
s= 22=2．
④：如图5中，当3＜t＜4时，重叠部分是△BEH．
s= （8﹣2t）2．
综上所述，s=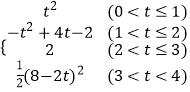 
【解析】解：（1）设抛物线的解析式为y=ax2+bx+c，
把O（0，0），A（2，﹣2），B（6，﹣2）代入得： ，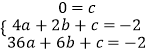
解得 ，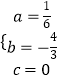
所以抛物线的解析式为： ．
（2）如图1中，当点O′与A重合时，点O′恰好在抛物线上．
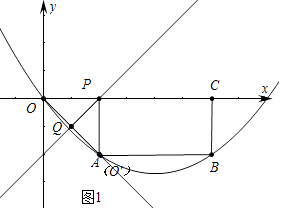
∵A（2，﹣2），
∴OA=2 ，OQ= ，OP=2，
∴t=1时，点O′在抛物线上．
所以答案是:（2）1．解：解：由题意A（2，﹣2），可知直线OA是第二四象限的角平分线，∠AOC=45°，PQ⊥OA，△OPQ与△O′PQ是全等的等腰直角三角形，OP=PO′=2t，PQ= 2 t
①：如图2中，当0＜t≤1时，重叠部分是△PQO′．
s=t2（0＜t≤1）
②：如图3中，当1＜t≤2时，重叠部分是四边形PQAH．
s= t t﹣ （2t﹣2）2=﹣t2+4t﹣2（1＜t≤2）
③：如图4中，当2＜t≤3时，重叠部分是△PEH．
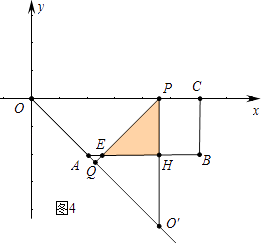
s= 22=2．
④：如图5中，当3＜t＜4时，重叠部分是△BEH．
s= （8﹣2t）2．
综上所述，s=
