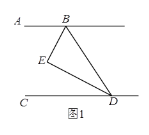��Ŀ����
����Ŀ����֪��������l1��y=��x2+bx+3��x���ڵ�A��B������A�ڵ�B����ࣩ����y���ڵ�C����Գ���Ϊx=1��������l2������A����x�����һ������ΪE��5��0������y���ڵ�D��0���� ![]() ����
����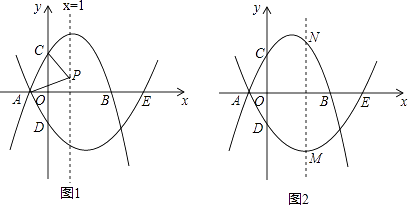
��1����������l2�ĺ�������ʽ��
��2��PΪֱ��x=1��һ���㣬����PA��PC����PA=PCʱ�����P�����ꣻ
��3��MΪ������l2��һ���㣬����M��ֱ��MN��y�ᣬ��������l1�ڵ�N�����M�Ե�A�˶�����E�Ĺ����У��߶�MN���ȵ����ֵ��
���𰸡�
��1���⣺��������l1��y=��x2+bx+3�ĶԳ���Ϊx=1��
�ੁ ![]() =1�����b=2��
=1�����b=2��
��������l1�Ľ���ʽΪy=��x2+2x+3��
��y=0���ɵé�x2+2x+3=0�����x=��1��x=3��
��A����������1��0����
��������l2������A��E���㣬
�����������l2����ʽΪy=a��x+1����x��5����
�֡�������l2��y���ڵ�D��0���� ![]() ����
����
�ੁ ![]() =��5a�����a=
=��5a�����a= ![]() ��
��
��y= ![]() ��x+1����x��5��=
��x+1����x��5��= ![]() x2��2x��
x2��2x�� ![]() ��
��
��������l2�ĺ�������ʽΪy= ![]() x2��2x��
x2��2x�� ![]()
��2���⣺��P������Ϊ��1��y�����ɣ�1���ɵ�C������Ϊ��0��3����
��PC2=12+��y��3��2=y2��6y+10��PA2=[1������1��]2+y2=y2+4��
��PC=PA��
��y2��6y+10=y2+4�����y=1��
��P��������1��1��
��3���⣺���������M��x�� ![]() x2��2x��
x2��2x�� ![]() ����
����
��MN��y�ᣬ
��N��x����x2+2x+3���� ![]() x2��2x��
x2��2x�� ![]()
�x2+2x+3= ![]() x2��2x��
x2��2x�� ![]() ���ɽ��x=��1��x=
���ɽ��x=��1��x= ![]() ��
��
�ٵ���1��x�� ![]() ʱ��MN=����x2+2x+3������
ʱ��MN=����x2+2x+3������ ![]() x2��2x��
x2��2x�� ![]() ��=��
��=�� ![]() x2+4x+
x2+4x+ ![]() =��
=�� ![]() ��x��
��x�� ![]() ��2+
��2+ ![]() ��
��
��Ȼ��1�� ![]() ��
�� ![]() ���൱x=
���൱x= ![]() ʱ��MN�����ֵ
ʱ��MN�����ֵ ![]() ��
��
�ڵ� ![]() ��x��5ʱ��MN=��
��x��5ʱ��MN=�� ![]() x2��2x��
x2��2x�� ![]() ��������x2+2x+3��=
��������x2+2x+3��= ![]() x2��4x��
x2��4x�� ![]() =
= ![]() ��x��
��x�� ![]() ��2��
��2�� ![]() ��
��
��Ȼ��x�� ![]() ʱ��MN��x�����������
ʱ��MN��x�����������
�൱x=5ʱ��MN�����ֵ�� ![]() ����5��
����5�� ![]() ��2��
��2�� ![]() =12��
=12��
���Ͽ�֪�ڵ�M�Ե�A�˶�����E�Ĺ����У��߶�MN���ȵ����ֵΪ12
����������1����������l1�ĶԳ���Ϊx=1���õ�b=2���õ�������l1�Ľ���ʽ���õ�A������Ϊ����1��0�����ɴ���ϵ�������������l2 �ĺ�������ʽ����2�����P�����꣬�ɣ�1���ɵ�C�����꣬��PC=PA���õ�P������Ϊ��1��1������3������������M������꣬��MN��y�ᣬ�õ�N�����꣬�ó�MN�����ֵ ![]() ���ڵ�
���ڵ� ![]() ��x��5ʱ ����Ȼ��x��
��x��5ʱ ����Ȼ��x�� ![]() ʱ��MN��x��������������Ե�x=5ʱ��MN�����ֵ�����Ͽ�֪�ڵ�M�Ե�A�˶�����E�Ĺ����У��߶�MN���ȵ����ֵΪ12���������ۺ��⣬�ѶȽϴ���ͽⷽ��ʱ��������ϸ.
ʱ��MN��x��������������Ե�x=5ʱ��MN�����ֵ�����Ͽ�֪�ڵ�M�Ե�A�˶�����E�Ĺ����У��߶�MN���ȵ����ֵΪ12���������ۺ��⣬�ѶȽϴ���ͽⷽ��ʱ��������ϸ.