题目内容
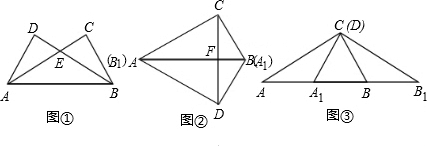
将两块大小一样含30°角的直角三角板,叠放在一起,使得它们的斜边AB重合,直角边不重合,已知AB=8,BC=AD=4,AC与BD相交于点E,连结CD。

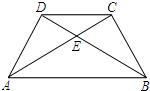
(1)填空:如图1,AC=______,BD=______;四边形ABCD是______梯形;
(2)请写出图1中所有的相似三角形(不含全等三角形);
(3)如图2,若以AB所在直线为轴,过点A垂直于AB的直线为轴建立如图2的平面直角坐标系,保持ΔABD不动,将ΔABC向轴的正方向平移到ΔFGH的位置,FH与BD相交于点P,设AF=t,ΔFBP面积为S,求S与t之间的函数关系式,并写出t的取值范围。
(2)请写出图1中所有的相似三角形(不含全等三角形);
(3)如图2,若以AB所在直线为轴,过点A垂直于AB的直线为轴建立如图2的平面直角坐标系,保持ΔABD不动,将ΔABC向轴的正方向平移到ΔFGH的位置,FH与BD相交于点P,设AF=t,ΔFBP面积为S,求S与t之间的函数关系式,并写出t的取值范围。
解:(1)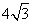 ; ;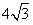 ;等腰; ;等腰;(2)共有9对相似三角形: ①△DCE、△ABE与△ACD或△BDC两两相似,分别是:△DCE∽△ABE,△DCE∽△ACD,△DCE∽△BDC,△ABE∽△ACD,△ABE∽△BDC;(有5对) ②△ABD∽△EAD,△ABD∽△EBC;(有2对) ③△BAC∽△EAD,△BAC∽△EBC;(有2对) 所以,一共有9对相似三角形。 |
|
| (3)由题意知,FP∥AE, ∴ ∠1=∠PFB, 又∵ ∠1=∠2=30°, ∴ ∠PFB=∠2=30°, ∴ FP=BP, 过点P作PK⊥FB于点K, 则 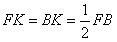 , ,∵ AF=t,AB=8, ∴ FB=8-t,  , ,在Rt△BPK中, 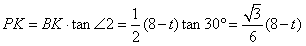 , ,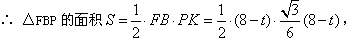 ∴ S与t之间的函数关系式为: 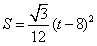 或 或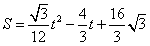 , ,t的取值范围是 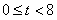 。 。 |
 |

练习册系列答案
相关题目
 C=AD=4,AC与BD相交于点E,连接CD.
C=AD=4,AC与BD相交于点E,连接CD.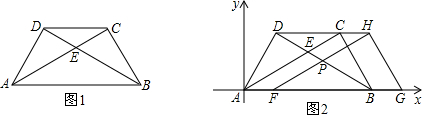
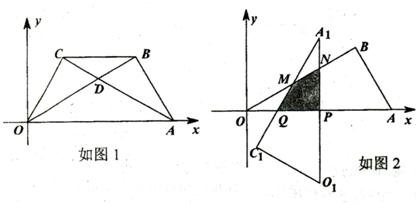
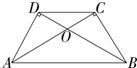 将两块大小一样含30°角的直角三角板如图叠放在一起,使它们的斜边AB重合,直角边不重合,当AB=8cm时,则两个直角顶点C、D的距离为
将两块大小一样含30°角的直角三角板如图叠放在一起,使它们的斜边AB重合,直角边不重合,当AB=8cm时,则两个直角顶点C、D的距离为