Question

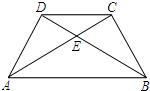
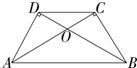将两块大小一样含30°角的直角三角板如图叠放在一起，使它们的斜边AB重合，直角边不重合，当AB=8cm时，则两个直角顶点C、D的距离为

 

cm．

Answer 1

分析：首先根据直角三角板的三角分别为30°，60°，90°，求得直角三角形△AOD，△BOC中的直角边与斜边的关系；根据两边对应成比例且夹角相等的三角形相似，易得△DOC∽△AOB，即可求得CD的长．

解答：解：∵∠DAB=∠CBA=60°，∠DBA=∠CAB=30°，
∴∠DAC=∠CBD=30°，
∵∠ADB=∠BCA=90°，
∴OD=

1

2

OA，OC=

1

2

OB，
∴

OD

OA

=

OC

OB

=

1

2

，
∵∠DOC=∠AOB，
∴△DOC∽△AOB，
∴CD：AB=OD：OA=1：2，
∵AB=8cm，
∴CD=4cm．

点评：此题考查了直角三角形的性质（直角三角形中，30°的角所对的直角边是斜边的一半）与相似三角形的判定与性质．解题的关键是准确识图．