题目内容
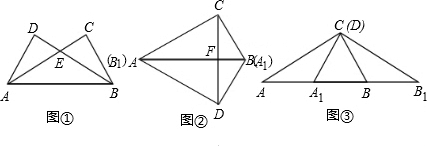
将两块大小一样含30°角的直角三角板,叠放在一起,使得它们的斜边AB重合,直角边不重合,已知AB=8,BC=AD=4,AC与BD相交于点E,连接CD.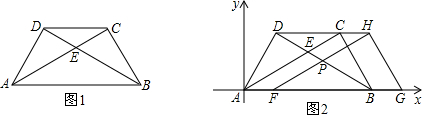
(1)填空:如图1,AC=
(2)请写出图1中所有的相似三角形;(不含全等三角形)
(3)如图2,若以AB所在直线为轴,过点A垂直于AB的直线为轴建立如图2的平面直角坐标系,保持△ABD不动,将△ABC向x轴的正方向平移到△FGH的位置,FH与BD相交于点P,设AF=t,△FBP面积为S,求S与t之间的函数关系式,并写出t的取值范围.
分析:(1)根据勾股定理可得AC=BD=
=4
;易知△ADC≌△BCD,利用四边形内角和是360°可得∠CDB=∠DCA=30°∵∠CAB=30°∴DC∥AB,∵AD=BC∴四边形ABCD是等腰梯形;
(2)图中的三角形分为两类:30°,30°,120°;30°,60°,90度.按此找相似三角形即可;
(3)过P作出△FBP的高.△FBP面积应等于FB×PK÷2,易得FB=AB-AF=8-k;则KB等于FB的一半,利用30°的正切值可求得FK的值.注意用t表示的线段应大于0.
| 82-42 |
| 3 |
(2)图中的三角形分为两类:30°,30°,120°;30°,60°,90度.按此找相似三角形即可;
(3)过P作出△FBP的高.△FBP面积应等于FB×PK÷2,易得FB=AB-AF=8-k;则KB等于FB的一半,利用30°的正切值可求得FK的值.注意用t表示的线段应大于0.
解答:解:(1)4
,4
,等腰;
(2)共有9对相似三角形.
①△DCE、△ABE与△ACD或△BDC两两相似,
分别是:△DCE∽△ABE,△DCE∽△ACD,△DCE∽△BDC,△ABE∽△ACD,△ABE∽△BDC;(有5对)
②△ABD∽△EAD,△ABD∽△EBC;(有2对)
③△BAC∽△EAD,△BAC∽△EBC;(有2对)
所以,一共有9对相似三角形.
(3)由题意知,FP∥AE,
∴∠1=∠PFB,
又∵∠1=∠2=30°,
∴∠PFB=∠2=30°,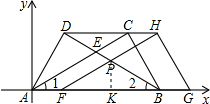
∴FP=BP
过点P作PK⊥FB于点K,则FK=BK=
FB.
∵AF=t,AB=8,
∴FB=8-t,BK=
(8-t).
在Rt△BPK中,PK=BK•tan∠2=
(8-t)tan30°=
(8-t).
∴△FBP的面积S=
•FB•PK=
(8-t)•
(8-t),
∴S与t之间的函数关系式为:
S=
(8-t)2,或S=
t2-
t+
,
t的取值范围为:0≤t<8.
| 3 |
| 3 |
(2)共有9对相似三角形.
①△DCE、△ABE与△ACD或△BDC两两相似,
分别是:△DCE∽△ABE,△DCE∽△ACD,△DCE∽△BDC,△ABE∽△ACD,△ABE∽△BDC;(有5对)
②△ABD∽△EAD,△ABD∽△EBC;(有2对)
③△BAC∽△EAD,△BAC∽△EBC;(有2对)
所以,一共有9对相似三角形.
(3)由题意知,FP∥AE,
∴∠1=∠PFB,
又∵∠1=∠2=30°,
∴∠PFB=∠2=30°,

∴FP=BP
过点P作PK⊥FB于点K,则FK=BK=
| 1 |
| 2 |
∵AF=t,AB=8,
∴FB=8-t,BK=
| 1 |
| 2 |
在Rt△BPK中,PK=BK•tan∠2=
| 1 |
| 2 |
| ||
| 6 |
∴△FBP的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 6 |
∴S与t之间的函数关系式为:
S=
| ||
| 12 |
| ||
| 12 |
4
| ||
| 3 |
| 16 |
| 3 |
| 3 |
t的取值范围为:0≤t<8.
点评:“有效的数学学习过程不能单纯地依赖模仿和记忆;有效的数学学习过程应引导学生主动地从事观察、实验、猜测、验证、推理与交流等数学活动,从而使学生形成自己对数学知识的理解和有效的学习策略”.此题正是在常见的三角板的操作变形中,将几何中的平移知识,代数中的函数知识有机地进行结合,要求学生抓住问题中的内在联系进行探究.

练习册系列答案
相关题目
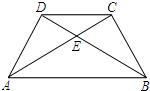 C=AD=4,AC与BD相交于点E,连接CD.
C=AD=4,AC与BD相交于点E,连接CD.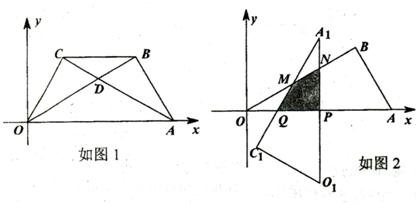
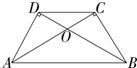 将两块大小一样含30°角的直角三角板如图叠放在一起,使它们的斜边AB重合,直角边不重合,当AB=8cm时,则两个直角顶点C、D的距离为
将两块大小一样含30°角的直角三角板如图叠放在一起,使它们的斜边AB重合,直角边不重合,当AB=8cm时,则两个直角顶点C、D的距离为