题目内容
将两块大小一样含30°角的直角三角板,叠放在一起,使得它们的斜边AB重合,直角边不重合,已知AB=8,B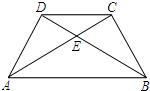 C=AD=4,AC与BD相交于点E,连接CD.
C=AD=4,AC与BD相交于点E,连接CD.(1)填空:如图,AC=
(2)请写出图中所有的相似三角形(不含全等三角形).
分析:(1)首先根据题意得:DC∥AB,∠ADB=∠ACB=90°,∠ABD=∠CAB=30°,然后由勾股定理,求得AC与BD的长,即可证得四边形ABCD是等腰梯形.
(2)根据两内角对应相等的三角形相似,即可证得.
(2)根据两内角对应相等的三角形相似,即可证得.
解答:解:(1)根据题意得:DC∥AB,∠ADB=∠ACB=90°,∠ABD=∠CAB=30°,
∵AB=8,BC=AD=4,
∴AC=BD=4
,∠DAB=∠CBA=60°,
∴四边形ABCD是等腰梯形;
(2)相似三角形有:△DCE∽△ABE,△DCE∽△DBC,△DBC∽△ABE,△DEA∽△DAB,△DEA∽△CBA,△CEB∽△DAB,△CEB∽△CBA,△ADC∽△AEB,△ADC∽△CED.
∵AB=8,BC=AD=4,
∴AC=BD=4
| 3 |
∴四边形ABCD是等腰梯形;
(2)相似三角形有:△DCE∽△ABE,△DCE∽△DBC,△DBC∽△ABE,△DEA∽△DAB,△DEA∽△CBA,△CEB∽△DAB,△CEB∽△CBA,△ADC∽△AEB,△ADC∽△CED.
点评:此题考查了相似三角形的判定与等腰梯形的判定,以及直角三角形的性质.此题难度不大,解题的关键是注意数形结合思想的应用.

练习册系列答案
相关题目
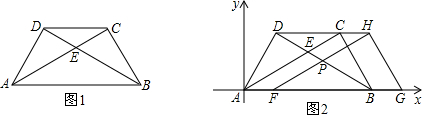
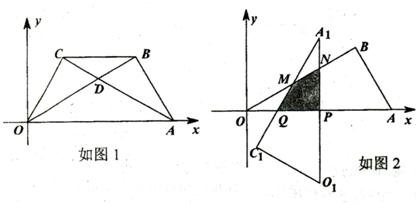
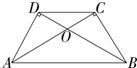 将两块大小一样含30°角的直角三角板如图叠放在一起,使它们的斜边AB重合,直角边不重合,当AB=8cm时,则两个直角顶点C、D的距离为
将两块大小一样含30°角的直角三角板如图叠放在一起,使它们的斜边AB重合,直角边不重合,当AB=8cm时,则两个直角顶点C、D的距离为