题目内容
17.如图①Rt△ABC中,∠C=90°,AC=BC=4,点D是AC的中点,点E是AB上一动点,做∠DEF=45°交BC于点F,连接DF,(1)直接写出图中的一对相似三角形;
(2)设AE=x,BF=y,求y与x的函数关系式;并计算当x当何值时,y有最值,最值是多少?
(3)如图②,若DE⊥AB,求出DF的长.
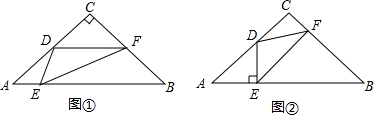
分析 (1)如图①中,△ADE∽△BEF.只要证明∠FEB=∠ADE即可.
(2)由△ADE∽△BEF,得$\frac{AD}{BE}$=$\frac{AE}{BF}$,即$\frac{2}{4\sqrt{2}-x}$=$\frac{x}{y}$,由此即可解决问题,再利用配方法求出最值即可.
(3)x=AE=DE=$\sqrt{2}$,由y=-$\frac{1}{2}$x2+2$\sqrt{2}$x=3,推出BF=3,CF=BC-BF=1,在Rt△CDF中,利用DF=$\sqrt{C{D}^{2}+C{F}^{2}}$即可解决问题.
解答 解:(1)如图①中,△ADE∽△BEF.理由如下:
∵CA=CB,∠C=90°,
∴∠A=∠B=45°,
∵∠DEB=∠A+∠ADE=∠DEF+∠FEB,∠DEF=∠A=45°,
∴∠FEB=∠ADE,
∴△ADE∽△BEF.
(2)∵AC=CB=4,∠C=90°,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=4$\sqrt{2}$,
∵D是AC中点,
∴AD=DC=2,
∵△ADE∽△BEF,
∴$\frac{AD}{BE}$=$\frac{AE}{BF}$,
∴$\frac{2}{4\sqrt{2}-x}$=$\frac{x}{y}$,
∴y=-$\frac{1}{2}$x2+2$\sqrt{2}$x,
∵y=-$\frac{1}{2}$x2+2$\sqrt{2}$x=-$\frac{1}{2}$(x-2$\sqrt{2}$)2+4,
∵-$\frac{1}{2}$<0,
∴x=2$\sqrt{2}$时,y有最大值4.
(3)如图②中,
∵DE⊥AB,
∴∠A=∠ADE=45°,
∵AD=DC=2,
∴x=AE=DE=$\sqrt{2}$,
∴y=-$\frac{1}{2}$x2+2$\sqrt{2}$x=3,
∴BF=3,CF=BC-BF=1,
在Rt△CDF中,DF=$\sqrt{C{D}^{2}+C{F}^{2}}$=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$.
点评 本题考查相似三角形综合题、二次函数的应用、勾股定理等知识,解题的关键是正确寻找相似三角形解决问题,学会构建二次函数解决最值问题,属于中考常考题型.

| A. | ax2+bx+c=0 | B. | 3x2+xy-y2=0 | C. | x2+x+1=0 | D. | x2+$\frac{1}{{x}^{2}}$=5 |
| A. | 三角形内角和180° | B. | 抛物线与x轴有2个交点 | ||
| C. | 若x2=4,则x=±2 | D. | 直径所对圆周角是100° |
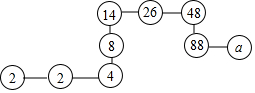 根据如图所示的规律.a的值为162.
根据如图所示的规律.a的值为162.