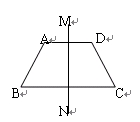
题目内容
如图14,在直角梯形ABCD中,AD∥BC,∠ABC=90°,∠C=60°,BC=2AD=2 ,点E是BC边的中点,△DEF是等边三角形,DF交AB于点G,则△BFG的周长为 __ .
,点E是BC边的中点,△DEF是等边三角形,DF交AB于点G,则△BFG的周长为 __ .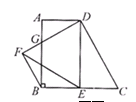
 ,点E是BC边的中点,△DEF是等边三角形,DF交AB于点G,则△BFG的周长为 __ .
,点E是BC边的中点,△DEF是等边三角形,DF交AB于点G,则△BFG的周长为 __ .
3+

已知AD∥BC,∠ABC=90°,点E是BC边的中点,即AD=BE=CE= ,
,
∴四边形ABED为平四边形,∴∠DEC=90°,∠A=90°,又∠C=60°,∴DE=CE•tan60°= ×
× =3,
=3,
又△DEF是等边三角形,∴DF=DE=AB=3,∠AGD=∠EDF=60°,∠ADG=30°
∴AG=AD•cot30°= ×
×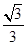 =1,∴DG=2,FG=DF-DG=1,BG=3-1=2,∴AG=FG=1,∠AGD=∠FGB,BG=DG=2,∴△AGD≌△BGF,∴BF=AD=
=1,∴DG=2,FG=DF-DG=1,BG=3-1=2,∴AG=FG=1,∠AGD=∠FGB,BG=DG=2,∴△AGD≌△BGF,∴BF=AD= ,∴△BFG的周长为2+1+
,∴△BFG的周长为2+1+ =3+
=3+ .
.
 ,
,∴四边形ABED为平四边形,∴∠DEC=90°,∠A=90°,又∠C=60°,∴DE=CE•tan60°=
 ×
× =3,
=3,又△DEF是等边三角形,∴DF=DE=AB=3,∠AGD=∠EDF=60°,∠ADG=30°
∴AG=AD•cot30°=
 ×
×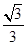 =1,∴DG=2,FG=DF-DG=1,BG=3-1=2,∴AG=FG=1,∠AGD=∠FGB,BG=DG=2,∴△AGD≌△BGF,∴BF=AD=
=1,∴DG=2,FG=DF-DG=1,BG=3-1=2,∴AG=FG=1,∠AGD=∠FGB,BG=DG=2,∴△AGD≌△BGF,∴BF=AD= ,∴△BFG的周长为2+1+
,∴△BFG的周长为2+1+ =3+
=3+ .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
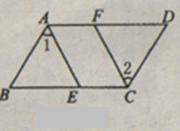
 ,则①
,则①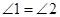 ,②
,②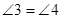 ,③
,③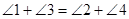 。上述结论中正确的是( )
。上述结论中正确的是( )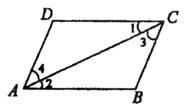
 A=
A=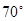 ,
,
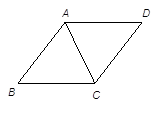
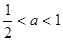 ),如图那样折一下,剪下一个边长等于矩形宽度的正方形;再把剩下的矩形如图那样折一下,剪下一个边长等于此时矩形宽度的正方形;如此操作下去,在第3次操作后,剩下的矩形恰好为正方形,则a的值为______.
),如图那样折一下,剪下一个边长等于矩形宽度的正方形;再把剩下的矩形如图那样折一下,剪下一个边长等于此时矩形宽度的正方形;如此操作下去,在第3次操作后,剩下的矩形恰好为正方形,则a的值为______.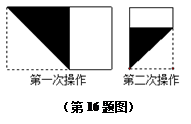
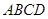 中,
中,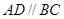 ,
,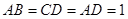 ,
,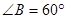 直线
直线 为梯形
为梯形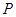 为
为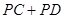 的最小值 。
的最小值 。